题目内容
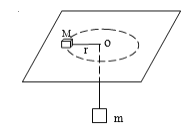
【题目】如图所示,细绳一端系着质量M=0.6kg的物体,静止在水平平台上,另一端通过光滑的小孔吊着质量m=0.3kg的物体,M与圆孔距离r=0.2m,并知M和水平面的最大静摩擦力为2N。现使此平面绕中心轴线转动,问角速度ω在什么范围m会处于静止状态?(g=l0m/s2)
【答案】2.9rad/s≤ω≤6.5rad/s
【解析】试题分析:设此平面角速度ω的最小值为ω1,此时M所受的静摩擦力达到最大,方向沿半径向外,则由牛顿第二定律得
T﹣fmax=M![]() ,
,
又T=mg
联立得 mg﹣fmax=M![]() ,
,
将m=0.3kg,fmax=2N,M=0.6kg,r=0.2m代入解得ω1=![]() rad/s
rad/s
设此平面角速度ω的最大值为ω2,此时M所受的静摩擦力达到最大,方向沿半径向里,则由牛顿第二定律得
T+fmax=M![]() ,
,
又T=mg
代入解得ω2=![]() rad/s
rad/s
故为使m处于静止状态,角速度ω的范围为:![]() .
.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目