题目内容
3.假设地球绕太阳运动时的轨道半径为r地,公转周期为T地,月球绕地球运动的轨道半径为r月,公转周期为T月,地球质量为M地,太阳质量为M阳,则关于轨道半径的三次方跟它的公转周期的二次方的比值k,下列说法不正确的是( )| A. | 地球绕太阳运动的${k_地}=\frac{{G{M_阳}}}{{4{π^2}}}$ | B. | 月球绕地球运动的${k_月}=\frac{{G{M_月}}}{{4{π^2}}}$ | ||
| C. | $\frac{k_地}{k_月}=\frac{M_阳}{M_地}$ | D. | k只与中心天体的质量有关 |
分析 万有引力提供向心力,应用牛顿第二定律列式求出轨道半径三次方与周期平方的关系,然后根据k的表达式分析答题.
解答 解:万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$(\frac{2π}{T})^{2}$r,整理得:$\frac{{r}^{3}}{{T}^{2}}$=$\frac{GM}{4{π}^{2}}$=k,
A、地球绕太阳运动的k地=$\frac{G{M}_{阳}}{4{π}^{2}}$,故A正确;
B、月球绕地球运动的k月=$\frac{G{M}_{地}}{4{π}^{2}}$,故B错误;
C、$\frac{{k}_{地}}{{k}_{月}}$=$\frac{\frac{G{M}_{阳}}{4{π}^{2}}}{\frac{G{M}_{地}}{4{π}^{2}}}$=$\frac{{M}_{阳}}{{M}_{地}}$,故C正确;
D、由k=$\frac{GM}{4{π}^{2}}$可知,k只与中心天体的质量有关,故D正确;
故选:ACD.
点评 本题考查了开普勒第三定律中k的影响因素,应用万有引力公式与牛顿第二定律可以解题.开普勒第三定律中的k与中心天体的质量有关.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列现象中,为了避免发生离心运动发生的是( )
| A. | 汽车过弯时要减速 | B. | 制作棉花糖 | ||
| C. | 洗衣机甩干衣物 | D. | 制作无缝钢管 |
11.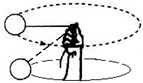 如图所示,手拉细线让小球在水平面内做圆周运动,忽略空气阻力,下列说法正确的是( )
如图所示,手拉细线让小球在水平面内做圆周运动,忽略空气阻力,下列说法正确的是( )
 如图所示,手拉细线让小球在水平面内做圆周运动,忽略空气阻力,下列说法正确的是( )
如图所示,手拉细线让小球在水平面内做圆周运动,忽略空气阻力,下列说法正确的是( )| A. | 小球受到重力、线的拉力和向心力三个力的作用 | |
| B. | 小球作匀变速曲线运动 | |
| C. | 当小球运动不断加快,小球在竖直方向上逐渐上升,最终可以上升至与细线在同一水平面 | |
| D. | 若手与细线打滑,随小球运动加快,小球将做离心运动 |
8.在下列情况中,物体的机械能不守恒的是(不计空气阻力)( )
| A. | 推出的铅球在空中运动的过程中 | B. | 飞船在椭圆轨道上绕地球运行 | ||
| C. | 沿着斜面匀速下滑的物体 | D. | 圆锥摆在水平内做匀速圆周运动 |
12.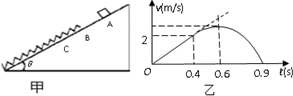 如图甲,倾角为θ的光滑斜面上放一轻质弹簧,其下端固定,静止时上端位置在B点,在A点放一质量m=2kg的小物块,小物块自由释放,在开始运动的一段时间内v-t图如图乙所示,小物块在0.4s时运动到B点,在0.9s时到达C点,BC的距离为1.2m(g取10m/s2).由图知( )
如图甲,倾角为θ的光滑斜面上放一轻质弹簧,其下端固定,静止时上端位置在B点,在A点放一质量m=2kg的小物块,小物块自由释放,在开始运动的一段时间内v-t图如图乙所示,小物块在0.4s时运动到B点,在0.9s时到达C点,BC的距离为1.2m(g取10m/s2).由图知( )
 如图甲,倾角为θ的光滑斜面上放一轻质弹簧,其下端固定,静止时上端位置在B点,在A点放一质量m=2kg的小物块,小物块自由释放,在开始运动的一段时间内v-t图如图乙所示,小物块在0.4s时运动到B点,在0.9s时到达C点,BC的距离为1.2m(g取10m/s2).由图知( )
如图甲,倾角为θ的光滑斜面上放一轻质弹簧,其下端固定,静止时上端位置在B点,在A点放一质量m=2kg的小物块,小物块自由释放,在开始运动的一段时间内v-t图如图乙所示,小物块在0.4s时运动到B点,在0.9s时到达C点,BC的距离为1.2m(g取10m/s2).由图知( )| A. | 斜面倾角θ=$\frac{π}{6}$ | |
| B. | C点处弹簧的弹性势能为16J | |
| C. | 物块从B运动到C的过程中机械能守恒 | |
| D. | 物块从C回到A的过程中,加速度先增大后减小,再保持不变 |
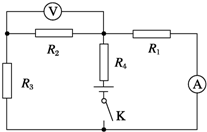 在如图所示电路中,已知R3=4Ω,闭合开关,电流表读数为0.75A,电压表读数为2V,经过一段时间,一个电阻被烧坏(断路),使电流表读数变为0.8A,电压表读数变为3.2V,问:
在如图所示电路中,已知R3=4Ω,闭合开关,电流表读数为0.75A,电压表读数为2V,经过一段时间,一个电阻被烧坏(断路),使电流表读数变为0.8A,电压表读数变为3.2V,问: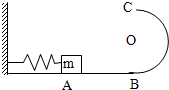 如图所示,光滑水平面AB与竖直面内的半圆形轨道在B点衔接,导轨半径为R,一个质量为m的静止物块在A处压缩弹簧,在弹力的作用下获某一向右速度,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动恰能完成半圆周运动到达C点,求
如图所示,光滑水平面AB与竖直面内的半圆形轨道在B点衔接,导轨半径为R,一个质量为m的静止物块在A处压缩弹簧,在弹力的作用下获某一向右速度,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动恰能完成半圆周运动到达C点,求