题目内容
一轻质弹簧直立在地面上，其劲度系数为k=400N/m，在弹簧的上端与空心物体A连接，物体B置于A内，B的上下表面恰与A接触，如图所示．A和B的质量均为1kg，先将A向上抬高使弹簧伸长5cm后从静止释放，A和B一起做上下方向的简谐运动，已知弹簧的弹性势能决定于弹簧形变大小（g取10m/s2，阻力不计）求：（1）物体A的振幅？
（2）物体B的最大速率？
（3）在最高点和最低点A对B的作用力？
（2）振子到达平衡位置时B的速率最大，从开始到平衡位置，运用机械能守恒定律列式，可求出B的最大速率．
（3）先由整体法求出加速度，再隔离B，运用牛顿第二定律求解．
代入数据解得△x=0.05m=5cm
开始释放时振子处在最大位移处，故振幅A为：A=5cm+5cm=10cm．
（2）由于开始时弹簧的伸长量恰等于振子在平衡位置时弹簧的压缩量，故弹性势能相等，设振子的最大速率为v，从开始到平衡位置，根据机械能守恒定律：
mg?A=
| 1 |
| 2 |
则得 v=
| 2gA |
（3）在最高点，振子受到的重力和弹力方向相同，根据牛顿第二定律：
对AB整体，有a=
| k△x+(mA+mB) |
| mA+mB |
A对B的作用力方向向下，其大小N1为：N1=mBa-mBg=10N
在最低点，振子受到的重力和弹力方向相反，根据牛顿第二定律：a=
| k(△x+A)-(mA+mB) |
| mA+mB |
A对B的作用力方向向上，其大小N2为：N2=mBa+mBg=30N
答：
（1）物体A的振幅是10cm．
（2）物体B的最大速率是1.4m/s．
（3）在最高点A对B的作用力方向向下，其大小为10N，在最低点A对B的作用力方向向上，其大小为30N．
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
一同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系。实验装置如下图甲所示，在离地面高为h的光滑水平桌面上，沿着与桌子右边缘垂直的方向放置一轻质弹簧，其左端固定，右端与质量为m的小刚球接触。将小球向左压缩弹簧一段距离后由静止释放，使小球沿水平方向射出桌面，小球在空中飞行落到位于水平地面的记录纸上留下痕迹。
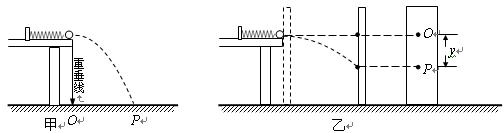
（1）若测得某次压缩弹簧释放后小球落点P痕迹到O点的距离为s，则释放小球前弹簧的弹性势能表达式为 ；
（2）该同学改变弹簧的压缩量进行多次测量得到下表一组数据：
| 弹簧压缩量x/cm | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
| 小球飞行水平距离s/m | 2.01 | 3.00 | 4.01 | 4.96 | 6.01 | 6.97 |
结合（1）问与表中数据，弹簧弹性势能与弹簧压缩量x之间的关系式应为 ；
（3）完成实验后，该同学对上述装置进行了如下图乙所示的改变：（I）在木板表面先后钉上白纸和复写纸，并将木板竖直立于靠近桌子右边缘处，使小球向左压缩弹簧一段距离后由静止释放，撞到木板并在白纸上留下痕迹O；（II）将木板向右平移适当的距离固定，再使小球向左压缩弹簧一段距离后由静止释放，撞到木板上得到痕迹P；（III）用刻度尺测量纸上O点到P点的竖直距离为y。若已知木板与桌子右边缘的水平距离为L，则（II）步骤中弹簧的压缩量应该为 ；
（4）若该同学在完成图乙实验的过程中，弹簧与桌子右边缘不垂直，用（3）问的方法计算得出的弹簧压缩量比实际 （选填“偏大”、“偏小”或“没有影响”）。
（8分）一同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系。实验装置如下图甲所示，在离地面高为h的光滑水平桌面上，沿着与桌子右边缘垂直的方向放置一轻质弹簧，其左端固定，右端与质量为m的小刚球接触。将小球向左压缩弹簧一段距离后由静止释放，使小球沿水平方向射出桌面，小球在空中飞行落到位于水平地面的记录纸上留下痕迹。
（1）若测得某次压缩弹簧释放后小球落点P痕迹到O点的距离为s，则释放小球前弹簧的弹性势能表达式为 ；
（2）该同学改变弹簧的压缩量进行多次测量得到下表一组数据：
| 弹簧压缩量x/cm | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
| 小球飞行水平距离s/m | 2.01 | 3.00 | 4.01 | 4.96 | 6.01 | 6.97 |
结合（1）问与表中数据，弹簧弹性势能与弹簧压缩量x之间的关系式应为 ；
（3）完成实验后，该同学对上述装置进行了如下图乙所示的改变：（I）在木板表面先后钉上白纸和复写纸，并将木板竖直立于靠近桌子右边缘处，使小球向左压缩弹簧一段距离后由静止释放，撞到木板并在白纸上留下痕迹O；（II）将木板向右平移适当的距离固定，再使小球向左压缩弹簧一段距离后由静止释放，撞到木板上得到痕迹P；（III）用刻度尺测量纸上O点到P点的竖直距离为y。若已知木板与桌子右边缘的水平距离为L，则（II）步骤中弹簧的压缩量应该为 ；
（4）若该同学在完成图乙实验的过程中，弹簧与桌子右边缘不垂直，用（3）问的方法计算得出的弹簧压缩量比实际 （选填“偏大”、“偏小”或“没有影响”）。
一同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系。实验装置如下图甲所示，在离地面高为h的光滑水平桌面上，沿着与桌子右边缘垂直的方向放置一轻质弹簧，其左端固定，右端与质量为m的小刚球接触。将小球向左压缩弹簧一段距离后由静止释放，使小球沿水平方向射出桌面，小球在空中飞行落到位于水平地面的记录纸上留下痕迹。
（1）若测得某次压缩弹簧释放后小球落点P痕迹到O点的距离为s，则释放小球前弹簧的弹性势能表达式为 ；
（2）该同学改变弹簧的压缩量进行多次测量得到下表一组数据：
| 弹簧压缩量x/cm | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
| 小球飞行水平距离s/m | 2.01 | 3.00 | 4.01 | 4.96 | 6.01 | 6.97 |
（3）完成实验后，该同学对上述装置进行了如下图乙所示的改变：（I）在木板表面先后钉上白纸和复写纸，并将木板竖直立于靠近桌子右边缘处，使小球向左压缩弹簧一段距离后由静止释放，撞到木板并在白纸上留下痕迹O；（II）将木板向右平移适当的距离固定，再使小球向左压缩弹簧一段距离后由静止释放，撞到木板上得到痕迹P；（III）用刻度尺测量纸上O点到P点的竖直距离为y。若已知木板与桌子右边缘的水平距离为L，则（II）步骤中弹簧的压缩量应该为 ；
（4）若该同学在完成图乙实验的过程中，弹簧与桌子右边缘不垂直，用（3）问的方法计算得出的弹簧压缩量比实际 （选填“偏大”、“偏小”或“没有影响”）。
