题目内容
 (2010?普陀区一模)倾角为θ=30°的斜面体放在水平地面上,一个重为G的球在水平力F的作用下,静止在光滑斜面上,则水平力F的大小为
(2010?普陀区一模)倾角为θ=30°的斜面体放在水平地面上,一个重为G的球在水平力F的作用下,静止在光滑斜面上,则水平力F的大小为
| ||
| 3 |
| ||
| 3 |
| ||
| 6 |
| ||
| 6 |
分析:先研究第一种情况:通过对小球出状态的分析,利用共点力平衡条件可求出水平力F的大小.
再研究力F方向变化后的情况:对小球受力分析,运用作图法求得力F与水平方向的角度,因为小球和斜面都处于静止状态,可对整体受力分析求出地面对斜面的摩擦力.
再研究力F方向变化后的情况:对小球受力分析,运用作图法求得力F与水平方向的角度,因为小球和斜面都处于静止状态,可对整体受力分析求出地面对斜面的摩擦力.
解答:解:对物体受力分析如图:
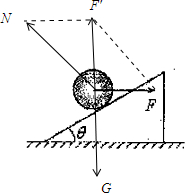
由平衡条件得:N与F的合力F′与重力G大小相等,
由三角函数关系得:F=Gtanθ
代入数据得:F=
G
转过角度后,由F大小不变,小球静止,支持力与F的合力不变,故此时转动后F转方向如图:
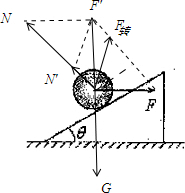
即:F转过的角度是2θ.
对整体受力分析并正交分解如图:
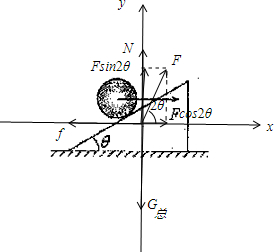
水平方向:f=Fcos2θ=
G
故答案为:
G,
G

由平衡条件得:N与F的合力F′与重力G大小相等,
由三角函数关系得:F=Gtanθ
代入数据得:F=
| ||
| 3 |
转过角度后,由F大小不变,小球静止,支持力与F的合力不变,故此时转动后F转方向如图:

即:F转过的角度是2θ.
对整体受力分析并正交分解如图:

水平方向:f=Fcos2θ=
| ||
| 6 |
故答案为:
| ||
| 3 |
| ||
| 6 |
点评:此题关键还是平衡条件的应用,难点在于选择合适的研究对象和找出力F转动后的角度,有难度,需要仔细推敲体会.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 (2010?普陀区一模)如图所示,光滑的斜劈放在水平面上,斜面上用固定的竖直板挡住一个光滑球,当整个装置沿水平面以速度v匀速运动时,以下说法中正确的是( )
(2010?普陀区一模)如图所示,光滑的斜劈放在水平面上,斜面上用固定的竖直板挡住一个光滑球,当整个装置沿水平面以速度v匀速运动时,以下说法中正确的是( ) (2010?普陀区一模)如图所示,叠放在一起的A、B两绝缘小物块放在水平向右的匀强电场中,其中B带正电q而A不带电,它们一切沿绝缘水平面以某一速度匀速运动.现突然使B带电量消失,同时A带上正电q,则A、B的运动状态可能为( )
(2010?普陀区一模)如图所示,叠放在一起的A、B两绝缘小物块放在水平向右的匀强电场中,其中B带正电q而A不带电,它们一切沿绝缘水平面以某一速度匀速运动.现突然使B带电量消失,同时A带上正电q,则A、B的运动状态可能为( ) (2010?普陀区一模)如图所示,两足够长的平行光滑的金属导轨MN、PQ相距为,导轨平面与水平面的夹角=30°,导轨电阻不计,磁感应强度为B的匀强磁场垂直于导轨平面向上.长为 的金属棒 垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为、电阻为r=R.两金属导轨的上端连接一个灯泡,灯泡的电阻RL=R,重力加速度为g.现闭合开关S,给金属棒施加一个方向垂直于杆且平行于导轨平面向上的、大小为F=mg的恒力,使金属棒由静止开始运动,当金属棒达到最大速度时,灯泡恰能达到它的额定功率.求:
(2010?普陀区一模)如图所示,两足够长的平行光滑的金属导轨MN、PQ相距为,导轨平面与水平面的夹角=30°,导轨电阻不计,磁感应强度为B的匀强磁场垂直于导轨平面向上.长为 的金属棒 垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为、电阻为r=R.两金属导轨的上端连接一个灯泡,灯泡的电阻RL=R,重力加速度为g.现闭合开关S,给金属棒施加一个方向垂直于杆且平行于导轨平面向上的、大小为F=mg的恒力,使金属棒由静止开始运动,当金属棒达到最大速度时,灯泡恰能达到它的额定功率.求: