��Ŀ����
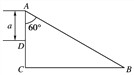
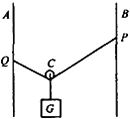
����Ŀ����ͼ��ʾ��ˮƽ��Ե���AB�봦����ֱƽ���ڵİ�Բ�ξ�Ե�⻬���BCƽ������,��Բ�ι���İ뾶R��0.4m��������ڿռ����ˮƽ���ҵ���ǿ�糡���糡ǿ��E��1.0��104 N/C������һ�����q��1.0��10��4 C������m��0.1kg�Ĵ�����(����Ϊ�ʵ�),��ˮƽ����ϵ�P���ɾ�ֹ�ͷ����������˶���Բ�ι����͵�Bʱ���ٶ���B��5 m/s����֪��������ˮƽ�����Ķ�Ħ������Ϊ0.5���������ٶ�g��10 m/s2����:

(1)�������˶���Բ�ι������͵�Bʱ��Բ�ι���Դ�����֧�����Ĵ�С;
(2)��������ˮƽ����ϵ��ͷŵ�P��B��ľ���;
(3)�������һ�ξ���C���������ˮƽ����ϵ�λ�õ�B��ľ�����
���𰸡���1��7.25N ��2��2.5m ��3��0.4m
�������������������1����B�㣬����ţ�ٵڶ����ɣ� ![]() �����FB=7.25N��
�����FB=7.25N��
��2����P�㵽B���ɶ��ܶ����� ![]() ���������ݽ�ã�x=2.5m
���������ݽ�ã�x=2.5m
��3����B�㵽C�㣬�ɶ��ܶ�����mg2R=![]()
��C��ɳ�ʱ��ˮƽ�������ȼ����˶��� ![]()
![]() ��
��
��ֱ���� ![]()
�������x=1.2m

 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д� Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�����Ŀ��һ��������ԭ��O�ɾ�ֹ������x����ֱ���˶���Ϊ�о������˶��Ĺ��ɶ���¼�����ڲ�ͬʱ�̵�λ�ú��ٶȣ�������ʾ������
ʱ��t/s | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
�����x/m | 0 | 0.5 | 2 | 4.5 | 8 | 12 | 16 | 20 |
˲ʱ�ٶ�v/��ms��1�� | 0 | 1 | 2 | 3 | 4 | 4 | 4 | 4 |
��1��������2sĩ���ٶȺ�5.5sĩ���ٶȣ�
��2����2s�ڵ�ƽ���ٶȺ�ǰ5s�ڵ�ƽ���ٶȣ�
��3��ǰ4s�ڵļ��ٶȣ�