题目内容
“投石机”是古代战争中常用的一种设备，它的结构可简化为如图所示的模型．某研学小组用自制的投石机演练投石过程．所用抛石机长臂的长度L=25/8m，质量m=12.0㎏的石块装在长臂末端的口袋中．开始时长臂与水平面间的夹角α=37°，对短臂施力，使石块经较长路径获得较大的速度，当长臂转到竖直位置时立即停止转动，石块被水平抛出，测得石块落地位置与抛出位置间的水平距离s=10m．不计空气阻力，重力加速度取g=10m/s2．求：（1）石块刚被投出时的速度大小v；
（2）石块刚落地时的速度vt的大小和方向；
（3）整个过程中投石机对石块所做的功W．
【答案】分析：（1）石块被投出后做平抛运动，根据水平距离和高度，求出石块刚被投出时的速度大小v；
（2）先求出石块刚落地时竖直方向分速度，再由速度合成求出速度vt的大小和方向；
（3）长臂从开始位置到竖直位置的过程中，重力做负功，投石机对石块做功，由动能定理求解投石机对石块所做的功W．
解答：
解：（1）石块被抛出后做平抛运动
水平方向 s=vt
竖直方向 h=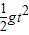
又h=L+Lsinα
解得 v=10m/s
（2）落地时，石块竖直方向的速度
vy=gt=10m/s
落地速度 vt=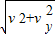
=10
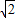m/s
设落地速度与水平方向间的夹角为θ，则有
tanθ=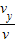
=1，得θ=45°
（3）长臂从开始位置到竖直位置的整个过程中，根据动能定理得
W-mgh=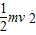
代入解得 W=1200J
答：（1）石块刚被投出时的速度大小v=10m/s；
（2）石块刚落地时的速度vt的大小为10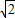
m/s，方向与水平方向间的夹角为45°；
（3）整个过程中投石机对石块所做的功W=1200J．
点评：本题是动能定理与平抛运动的综合应用，平抛运动采用运动的合成和分解的方法研究，运用动能定理求变力做功，都是经常运用的方法．
（2）先求出石块刚落地时竖直方向分速度，再由速度合成求出速度vt的大小和方向；
（3）长臂从开始位置到竖直位置的过程中，重力做负功，投石机对石块做功，由动能定理求解投石机对石块所做的功W．
解答：
解：（1）石块被抛出后做平抛运动水平方向 s=vt
竖直方向 h=
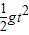
又h=L+Lsinα
解得 v=10m/s
（2）落地时，石块竖直方向的速度
vy=gt=10m/s
落地速度 vt=
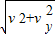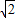=10m/s设落地速度与水平方向间的夹角为θ，则有
tanθ=
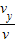=1，得θ=45°（3）长臂从开始位置到竖直位置的整个过程中，根据动能定理得
W-mgh=
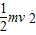
代入解得 W=1200J
答：（1）石块刚被投出时的速度大小v=10m/s；
（2）石块刚落地时的速度vt的大小为10
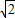m/s，方向与水平方向间的夹角为45°；（3）整个过程中投石机对石块所做的功W=1200J．
点评：本题是动能定理与平抛运动的综合应用，平抛运动采用运动的合成和分解的方法研究，运用动能定理求变力做功，都是经常运用的方法．
练习册系列答案
相关题目
“投石机”是古代战争中常用的一种设备，它的结构可简化为如图所示的模型．某研学小组用自制的投石机演练投石过程．所用抛石机长臂的长度L=25/8m，质量m=12.0㎏的石块装在长臂末端的口袋中．开始时长臂与水平面间的夹角α=37°，对短臂施力，使石块经较长路径获得较大的速度，当长臂转到竖直位置时立即停止转动，石块被水平抛出，测得石块落地位置与抛出位置间的水平距离s=10m．不计空气阻力，重力加速度取g=10m/s2．求：
