题目内容
【题目】如图所示为研究电子枪中电子在电场中运动的简化模型示意图．在xoy平面的第一象限，存在以
轴、
轴及双曲线
的一段（0≤≤L,0≤≤L）为边界的匀强电场区域Ⅰ；在第二象限存在以＝－L、＝－2L、＝0、＝L为边界的匀强电场区域Ⅱ．两个电场大小均为E，不计电子所受重力，电子的电荷量大小为e，则：
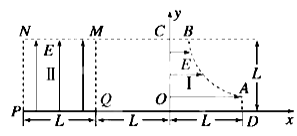
（1）从电场Ⅰ的边界B点处静止释放电子，电子离开MNPQ时的位置坐标；
（2）从电场I的AB曲线边界处由静止释放电子，电子离开MNPQ时的最小动能；
（3）若将左侧电场II整体水平向左移动
（n≥1），要使电子从=-2L，=0处离开电场区域II，在电场I区域内由静止释放电子的所有位置。
【答案】（1）（-2L,0）；（2）EeL；（3）
【解析】
试题分析：（1）关于B点，其纵坐标y=L，根据
，相应横坐标
当电子加速到y轴C位置时，
，解得
电子以速度v进入电场区域Ⅱ，做类平抛运动
有L=vt, 
解得：h=L即电子恰从P点射出，坐标为（-2L,0）
（2）设释放位置坐标为（x，y）
根据动能定理
; L=vt ；
解得：
即所有从边界AB曲线上由静止释放的电子均从P点射出
从边界AB出发到P点射出的全过程，由动能定理：Ek=Ee（x+y）
因为
，所以当x=y=L/2时，动能EK有最小值Ek=EeL．
（3）设释放位置坐标为（x，y），
，
，
，
解得：
练习册系列答案
相关题目
