题目内容
3.地球同步卫星轨道半径约为地球半径的6.6倍,设月球密度与地球相同,试估算:绕月心在月球表面附近做圆周运动的探月探测器的运行周期约为多少小时?分析 根据万有引力提供向心力,表示出卫星运行的周期,根据地球同步卫星轨道半径约为地球半径的6.6倍求出地球表面附近做圆周运动的卫星运行周期.
根据万有引力提供向心力,表示出中心体的质量,再根据月球密度与地球相同,求出绕月球表面附近做圆周运动的探月探测器的运行周期和地球表面附近做圆周运动的卫星运行周期的关系.
解答 解:根据万有引力提供向心力,$\frac{GMm}{{r}^{2}}$=m$\frac{4{π}^{2}r}{{T}^{2}}$
解得:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$
地球同步卫星轨道半径约为地球半径的6.6倍,
所以地球表面附近做圆周运动的卫星运行周期与地球同步卫星的周期之比是:$\frac{{T}_{地表}}{{T}_{同}}$=$\sqrt{\frac{1}{6.{6}^{3}}}$
地球同步卫星的周期是24h.
解得:T地表=1.4h
根据星球表面的卫星万有引力提供向心力得,$\frac{GMm}{{R}^{2}}$=m$\frac{4{π}^{2}R}{{T}^{2}}$
则有M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$
密度ρ=$\frac{M}{V}$=$\frac{\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}}{\frac{4π{R}^{3}}{3}}$=$\frac{3π}{G{T}^{2}}$
T为星球表面运行的卫星周期.
月球密度与地球相同,所以绕月球表面附近做圆周运动的探月探测器的运行周期和地球表面附近做圆周运动的卫星运行周期相同.
所以绕月球表面附近做圆周运动的探月探测器的运行周期约为1.4h.
答:月心在月球表面附近做圆周运动的探月探测器的运行周期约为1.4h.
点评 此题一定明确万有引力提供向心力,会用周期表示向心力,还要知道球体的体积公式及密度公式,同时注意公式间的化简.

 名校课堂系列答案
名校课堂系列答案 如图所示,在真空中,两个放在绝缘架上的相同金属小球A和B,相距为r.球的半径比r小得多,A带电荷量为+5Q,B带电荷量为-Q,相互作用的静电力为F.现将小球A和B互相接触后,再移回至原来各自的位置,这时A和B之间相互作用的静电力为F′.则F与F′之比为( )
如图所示,在真空中,两个放在绝缘架上的相同金属小球A和B,相距为r.球的半径比r小得多,A带电荷量为+5Q,B带电荷量为-Q,相互作用的静电力为F.现将小球A和B互相接触后,再移回至原来各自的位置,这时A和B之间相互作用的静电力为F′.则F与F′之比为( )| A. | 4:5 | B. | 5:4 | C. | 5:9 | D. | 9:5 |
 将带正电的小球a放在绝缘支架上,完全相同的小球b、c用绝缘细线系在支架上,小球b、c的质量和所带电荷量均相等,如图所示,其中∠α>∠β,不考虑b、c间的相互作用.由图可得( )
将带正电的小球a放在绝缘支架上,完全相同的小球b、c用绝缘细线系在支架上,小球b、c的质量和所带电荷量均相等,如图所示,其中∠α>∠β,不考虑b、c间的相互作用.由图可得( )| A. | 小球b、c带负电 | |
| B. | 小球b、c带正电 | |
| C. | 小球b受到的库仑力大于小球c受到的库仑力 | |
| D. | 在其他条件不变时,两带电小球间的距离越大,带电小球所受的库仑力越小 |
 如图所示,质量为3m足够长的绝缘小车静止在光滑水地面上,其光滑的上表面有一质量为m可视为质点的小滑块,静止时滑块距小车右边挡板的距离为l,滑块带有电荷量为q的正电荷,现加一水平向右,场强为E的匀强电场,于是带电滑块由静止开始向右运动,并与小车右边的挡板发生碰撞,设碰撞的时间极短,碰撞过没有动能损失,且滑块的电荷量保持不变,求;
如图所示,质量为3m足够长的绝缘小车静止在光滑水地面上,其光滑的上表面有一质量为m可视为质点的小滑块,静止时滑块距小车右边挡板的距离为l,滑块带有电荷量为q的正电荷,现加一水平向右,场强为E的匀强电场,于是带电滑块由静止开始向右运动,并与小车右边的挡板发生碰撞,设碰撞的时间极短,碰撞过没有动能损失,且滑块的电荷量保持不变,求;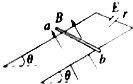 如图所示,两平行金属导轨间的距离L=0.40m,金属导轨所在的平面与水平面夹角θ=37°,在导轨所在平面内,分布着磁感应强度B=0.50T、方向垂直于导轨所在平面的匀强磁场.金属导轨的一端接有电动势E=4.5V、内阻r=0.50Ω的直流电源.现把一个质量m=0.04kg的导体棒ab放在金属导轨上,导体棒恰好静止.导体棒与金属导轨垂直且接触良好,导体棒与金属导轨接触的两点间的电阻R0=2.5Ω,金属导轨电阻不计,g取10m/s2.已知sin37°=0.60,cos37°=0.80,求:
如图所示,两平行金属导轨间的距离L=0.40m,金属导轨所在的平面与水平面夹角θ=37°,在导轨所在平面内,分布着磁感应强度B=0.50T、方向垂直于导轨所在平面的匀强磁场.金属导轨的一端接有电动势E=4.5V、内阻r=0.50Ω的直流电源.现把一个质量m=0.04kg的导体棒ab放在金属导轨上,导体棒恰好静止.导体棒与金属导轨垂直且接触良好,导体棒与金属导轨接触的两点间的电阻R0=2.5Ω,金属导轨电阻不计,g取10m/s2.已知sin37°=0.60,cos37°=0.80,求: