题目内容
【题目】如图所示，原长分别为L1和L2 ， 劲度系数分别为k1、k2的轻弹簧竖直悬挂在天花板上，两弹簧之间有一质量为m1的物体，最下端挂着质量为m2的另一物体，整个装置处于静止状态，求：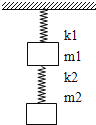
（1）这时两弹簧的总长．
（2）若用一个质量为M的平板把下面的物体竖直缓慢的向上托起，直到两弹簧的总长度等于两弹簧的原长之和，求这时平板受到下面物体的压力．
【答案】
（1）
以m1m2整体为研究对象进行受力分析，根据平衡条件有：
k1△x1=m1g+m2g ①
以m2为研究对象，有：m2g=k2△x2 ②
两弹簧的总长L=L1+L2+△x1+△x2 ③
联立①②③得： 
（2）
当两个弹簧的总长度等于两弹簧原长之和时，下面弹簧的压缩量应等于上面弹簧的伸长量，设为x，
对m1受力分析得：m1g=k1x+k2x
对平板和m1整体受力分析得
受力分析得：m1g=k1x+k2x
对平板和m1整体受力分析得：
FN=m2g+k2x
根据牛顿第三定律，有
FN′=FN
解得： 
【解析】（1）以m1m2整体为研究对象进行受力分析，根据平衡条件有：
k1△x1=m1g+m2g ①
以m2为研究对象，有：m2g=k2△x2②
两弹簧的总长L=L1+L2+△x1+△x2 ③
联立①②③得： （2）当两个弹簧的总长度等于两弹簧原长之和时，下面弹簧的压缩量应等于上面弹簧的伸长量，设为x ，
对m1受力分析得：m1g=k1x+k2x
对平板和m1整体受力分析得
受力分析得：m1g=k1x+k2x
对平板和m1整体受力分析得：
FN=m2g+k2x
根据牛顿第三定律，有
FN′=FN
解得：
（1）整体法受力分析根据胡克定律求上面弹簧的长，然后隔离法对m2受力分析根据胡克定律求下面弹簧的长度（2）当两个弹簧的总长度等于两弹簧原长之和时，上边弹簧的伸长量与下边弹簧的压缩量相等．对m1受力分析，有m1g=k1x+k2x ， 得出伸长量和压缩量x ． 对物体m2受力分析有：FN=m2g+k2x ， 再结合牛顿第三定律，求出物体对平板的压力FN′．
