题目内容
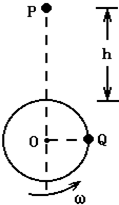
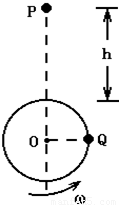
如图所示,小球Q在竖直平面内做匀速圆周运动,当Q球转到图示位置时,有另一小球P在距圆周最高点为h处开始自由下落,要使两球在圆周的最高点相碰,则Q球的角速度ω满足什么条件?
【答案】分析:小球P自由下落的高度是h,下落时间为t= .要使两球在圆周的最高点相碰,在小球P下落h高度的时间内,Q球转过时间为t=nT+
.要使两球在圆周的最高点相碰,在小球P下落h高度的时间内,Q球转过时间为t=nT+ (n=0,1,2,3…),T=
(n=0,1,2,3…),T= ,求解角速度ω.
,求解角速度ω.
解答:解:小球P自由落体运动的时间为t,则有: 得到
得到 
Q球运动到最高点的可能时间为:
由于t=t'
解得,角速度 (n=0,1,2,3…)
(n=0,1,2,3…)
答:Q球的角速度ω满足的条件是: (n=0,1,2,3…).
(n=0,1,2,3…).
点评:本题关键要抓住两球运动的同时性和圆周运动的周期性;得到的角速度是通项,不是一个特殊值.
 .要使两球在圆周的最高点相碰,在小球P下落h高度的时间内,Q球转过时间为t=nT+
.要使两球在圆周的最高点相碰,在小球P下落h高度的时间内,Q球转过时间为t=nT+ (n=0,1,2,3…),T=
(n=0,1,2,3…),T= ,求解角速度ω.
,求解角速度ω.解答:解:小球P自由落体运动的时间为t,则有:
 得到
得到 
Q球运动到最高点的可能时间为:

由于t=t'
解得,角速度
 (n=0,1,2,3…)
(n=0,1,2,3…)答:Q球的角速度ω满足的条件是:
 (n=0,1,2,3…).
(n=0,1,2,3…).点评:本题关键要抓住两球运动的同时性和圆周运动的周期性;得到的角速度是通项,不是一个特殊值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
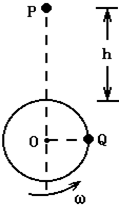 如图所示,小球Q在竖直平面内做匀速圆周运动,当Q球转到图示位置时,有另一小球P在距圆周最高点为h处开始自由下落,要使两球在圆周的最高点相碰,则Q球的角速度ω满足什么条件?
如图所示,小球Q在竖直平面内做匀速圆周运动,当Q球转到图示位置时,有另一小球P在距圆周最高点为h处开始自由下落,要使两球在圆周的最高点相碰,则Q球的角速度ω满足什么条件?