题目内容
3.小船在宽度为300m,水流速度为5m/s的河中驶向对岸,已知小船在静水中的速度为10m/s,两岸是平行的,求:(1)若要使小船最短时间过河,它将在何时何处到达对岸?
(2)若要使小船到达正对岸,最短位移为?小船应如何行驶?要用多长时间?
分析 (1)当船在垂直于河岸方向上的速度最大时,渡河时间最短,即为船头始终指向河对岸时,时间最短.用运动学公式即可得知渡河的最短时间,船还随河水向下运动,求出船随河水向下运动的位移,即可得知船的实际位移.
(2)船垂直渡河时船的航程最短,此时船头要指向上游,并且沿河岸方向上的分量大小与水流的速度大小相等,对两个速度进行合成,利用运动学公式即可求得渡河时间.
解答 解:(1)船渡河时间最短,就是在垂直于河岸方向上的速度最大,即为让船头始终指向对岸,渡河时间为:
tmin=$\frac{d}{{v}_{c}}$=$\frac{300}{10}$=30s
船沿河流方向上的位移为:s=v水•tmin=5×30=150m (2)要使船航程最短,即为让船垂直河岸渡河,船航行的实际速度垂直于河岸,如图所示
(2)要使船航程最短,即为让船垂直河岸渡河,船航行的实际速度垂直于河岸,如图所示
设船在静水中的速度方向与河岸间的夹角为θ,船在静水中的速度沿河岸上的分量大小与水流的速度大小相等,方向相反,有:v静•cosθ=v水
即为:cosθ=$\frac{5}{10}$
得:θ=60°
即为船头指向上游,与河岸间的夹角为60°
此时合速度为:v合=$\sqrt{1{0}^{2}-{5}^{2}}$=5$\sqrt{3}$m/s
渡河时间为:t=$\frac{d}{{v}_{合}}$=$\frac{300}{5\sqrt{3}}$=20$\sqrt{3}$s
答:(1)若要使小船最短时间过河,它将在30s,到达偏离正对岸下游150m;
(2)若要使小船到达正对岸,最短位移为300m,小船应偏向上游,要用20$\sqrt{3}$s时间.
点评 该题通过渡河的模型考察了运动的合成与分解,关于渡河问题,应注意几种渡河方式,一是垂直渡河,此时渡河位移最短,但是所用时间不是最短的,此种情况要求船的合速度与河岸垂直,二是船头始终指向对岸的渡河,此种情况下渡河时间最短,但是渡河位移不是最短;关于渡河问题,还要会判断能否垂直渡河,其条件是船在静水中的速度大小要大于河水流动的速度大小.

 如图所示,在水平面上,质量相等的物体A、B材料相同,中间用一根轻质弹簧相连.现用水平拉力F作用在B上,从静止开始经过一段时间后,A、B一起做匀加速直线运动,速度达到V时,它们的总动能为EK.撤掉水平力F,最后系统停止运动.(最大静摩擦力等于滑动摩擦力) 从撤掉拉力F到系统停止运动的过程中,系统( )
如图所示,在水平面上,质量相等的物体A、B材料相同,中间用一根轻质弹簧相连.现用水平拉力F作用在B上,从静止开始经过一段时间后,A、B一起做匀加速直线运动,速度达到V时,它们的总动能为EK.撤掉水平力F,最后系统停止运动.(最大静摩擦力等于滑动摩擦力) 从撤掉拉力F到系统停止运动的过程中,系统( )| A. | 克服阻力做的功一定等于系统的初动能EK | |
| B. | 克服阻力做的功一定大于系统的初动能EK | |
| C. | 克服阻力做的功可能小于系统的初动能EK | |
| D. | 克服阻力做的功可能等于系统的机械能的减少量 |
| A. | 3 s内的位移是12 m | B. | 3 s内的位移是9 m | ||
| C. | 1 s末速度的大小是6 m/s | D. | 3 s末速度的大小是6 m/s |
| A. | 0 | B. | 225J | C. | 400J | D. | 无法计算 |

| A. | 物体的初速度是3 m/s | |
| B. | 物体的加速度大小为1.5 m/s2 | |
| C. | 2 s末物体运动方向发生变化 | |
| D. | 前2 s的加速度与后2 s的加速度方向相反 |
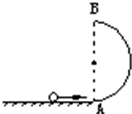 AB为竖直半圆轨道的竖直直径,轨道半径R=0.5m.轨道A端水平面相切.质量为1kg的光滑小球从水平面上以初速度vo=2$\sqrt{10}$m/s.向A滑动(A为半圆轨道的最低点).
AB为竖直半圆轨道的竖直直径,轨道半径R=0.5m.轨道A端水平面相切.质量为1kg的光滑小球从水平面上以初速度vo=2$\sqrt{10}$m/s.向A滑动(A为半圆轨道的最低点). 甲要把一个量程为200μA的直流电流计G,改装成量范围是0~4V的直流电压表.
甲要把一个量程为200μA的直流电流计G,改装成量范围是0~4V的直流电压表.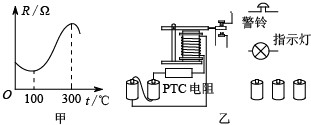 PTC是一种新型的半导体陶瓷材料,它以钛酸钡为主,渗入多种物质后加工而成,目前家用的陶瓷暖风器、陶瓷电热水壶等就是用这种材料做成的.PTC有一个根据需要设定的温度,低于这个温度时,其电阻随温度的升高而减小,高于这个温度时,电阻值则随温度的升高而增大,我们把这个设定的温度叫“居里点温度”,用PTC材料制成的电热器具有发热、控温双重功能,应用十分广泛.
PTC是一种新型的半导体陶瓷材料,它以钛酸钡为主,渗入多种物质后加工而成,目前家用的陶瓷暖风器、陶瓷电热水壶等就是用这种材料做成的.PTC有一个根据需要设定的温度,低于这个温度时,其电阻随温度的升高而减小,高于这个温度时,电阻值则随温度的升高而增大,我们把这个设定的温度叫“居里点温度”,用PTC材料制成的电热器具有发热、控温双重功能,应用十分广泛.