题目内容
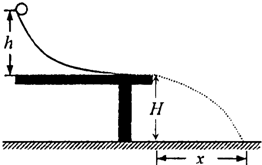 一同学利用如图所示的实验装置验证机械能守恒定律.该弧形轨道的末端水平,离地面的高度为H.现将一钢球从轨道的某一高度h处由静止释放,钢球的平均落点距离轨道末端的水平距离为x.
一同学利用如图所示的实验装置验证机械能守恒定律.该弧形轨道的末端水平,离地面的高度为H.现将一钢球从轨道的某一高度h处由静止释放,钢球的平均落点距离轨道末端的水平距离为x.(1)若实验所测得的数据在误差范围内满足x2=
(2)实际上轨道是不光滑的,钢球下滑过程需要克服摩擦力做功,已知测得钢球的质量为m,则钢球在下滑过程中克服摩擦力做功大小为
分析:(1)现根据小球离开桌面后做平抛运动求得小球离开桌面时的速度,再根据小球在斜槽上运动过程中机械能守恒,求得表达式.
(2)轨道若不光滑,根据动能动能定理列式求解.
(2)轨道若不光滑,根据动能动能定理列式求解.
解答:解:(1)小球离开桌面后做平抛运动,有
x=v0t
H=
gt2
则小球离开桌面时的速度为v0=x
若实验所测得的数据在误差范围内,则小球在斜槽上运动过程中机械能守恒,根据机械能守恒定律有
mgh=
mv02
即mgh=
m(x
)2
所以mgh=
mx2
解得x2=4Hh
(2)若轨道是不光滑的,钢球下滑过程需要克服摩擦力做功,根据动能定理有
mgh+Wf=
m(x
)2
解得Wf=mgh-
则钢球在下滑过程中克服摩擦力做功大小为mgh-
.
故答案为:(1)4Hh,(2)mgh-
.
x=v0t
H=
| 1 |
| 2 |
则小球离开桌面时的速度为v0=x
|
若实验所测得的数据在误差范围内,则小球在斜槽上运动过程中机械能守恒,根据机械能守恒定律有
mgh=
| 1 |
| 2 |
即mgh=
| 1 |
| 2 |
|
所以mgh=
| 1 |
| 2 |
| g |
| 2H |
解得x2=4Hh
(2)若轨道是不光滑的,钢球下滑过程需要克服摩擦力做功,根据动能定理有
mgh+Wf=
| 1 |
| 2 |
|
解得Wf=mgh-
| mgx2 |
| 4H |
则钢球在下滑过程中克服摩擦力做功大小为mgh-
| mgx2 |
| 4H |
故答案为:(1)4Hh,(2)mgh-
| mgx2 |
| 4H |
点评:本题从新的角度考查了对机械能守恒实定律的理解,有一定的创新性,很好的考查了学生的创新思维.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
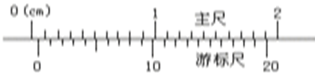 (2010?宁河县一模)(1)如图,用游标卡尺观察光的衍射现象时,调节游标尺和主尺两测脚间的距离如图所示.则形成的狭缝宽为
(2010?宁河县一模)(1)如图,用游标卡尺观察光的衍射现象时,调节游标尺和主尺两测脚间的距离如图所示.则形成的狭缝宽为
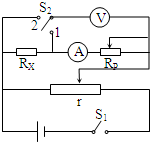 的频率为f,根据这些条件计算重锤下落加速度a的表达式为a=
的频率为f,根据这些条件计算重锤下落加速度a的表达式为a=


 =__________(用H、h表示),
=__________(用H、h表示),