题目内容
3. 如图所示,A、B两物体用轻绳相连,轻绳的最大拉力为100N,mA=4kg,mB=8kg,在拉力F的作用下A、B一起向上加速运动,为使轻绳不被拉断,则F允许的最大值是(g=10m/s2)( )
如图所示,A、B两物体用轻绳相连,轻绳的最大拉力为100N,mA=4kg,mB=8kg,在拉力F的作用下A、B一起向上加速运动,为使轻绳不被拉断,则F允许的最大值是(g=10m/s2)( )| A. | 120N | B. | 150N | C. | 270N | D. | 240N |
分析 隔离对B分析,结合最大拉力,运用牛顿第二定律求出临界加速度,再对整体分析,根据牛顿第二定律求出F的最大值.
解答 解:隔离对B分析,B的最大加速度为:
${a}_{m}=\frac{{T}_{m}-{m}_{B}g}{{m}_{B}}=\frac{100-80}{8}m/{s}^{2}$=2.5m/s2;
对整体分析,根据牛顿第二定律得:
F-(mA+mB)g=(mA+mB)am,
解得最大拉力为:
F=(mA+mB)(g+am)=12×12.5N=150N.
故选:B.
点评 本题考查了牛顿第二定律的临界极值问题,关键抓住临界状态,通过隔离法求出加速度,再通过整体法进行求解,难度不大.

练习册系列答案
相关题目
3.下列对做曲线运动物体的运动情况的描述中,正确的是( )
| A. | 物体的运动轨迹一定是一条曲线 | B. | 物体的速度大小必定不断变化 | ||
| C. | 物体的速度方向必定不断变化 | D. | 物体的加速度可能等于零 |
11. 如图所示,t=0时刻一物块靠着竖直粗糙墙面从A点开始下滑,同时给物块施加水平向左的作用力F,F随时间的关系是F=5t,物块与墙面的动摩擦因数是μ=0.4,物块质量m=0.5kg.t=2.5s时物块到达B点,t=6s时物块在C点.g=10m/s2.则此过程( )
如图所示,t=0时刻一物块靠着竖直粗糙墙面从A点开始下滑,同时给物块施加水平向左的作用力F,F随时间的关系是F=5t,物块与墙面的动摩擦因数是μ=0.4,物块质量m=0.5kg.t=2.5s时物块到达B点,t=6s时物块在C点.g=10m/s2.则此过程( )
 如图所示,t=0时刻一物块靠着竖直粗糙墙面从A点开始下滑,同时给物块施加水平向左的作用力F,F随时间的关系是F=5t,物块与墙面的动摩擦因数是μ=0.4,物块质量m=0.5kg.t=2.5s时物块到达B点,t=6s时物块在C点.g=10m/s2.则此过程( )
如图所示,t=0时刻一物块靠着竖直粗糙墙面从A点开始下滑,同时给物块施加水平向左的作用力F,F随时间的关系是F=5t,物块与墙面的动摩擦因数是μ=0.4,物块质量m=0.5kg.t=2.5s时物块到达B点,t=6s时物块在C点.g=10m/s2.则此过程( )| A. | 物块的最大加速度是10m/s2 | B. | 物块先加速再减速 | ||
| C. | 物块在B点时的速度是12.5m/s | D. | 物块在t=6s时的摩擦力是12N |
18. 如图是汽车运送圆柱形工件的示意图.图中P、Q、N是固定在车体上的压力传感器,假设圆柱形工件表面光滑,汽车静止在水平地面上不动时Q传感器示数为零,P、N传感器示数不为零.现该汽车正沿倾角为15°的斜面向上匀加速启动,P传感器示数为零而Q、N传感器示数不为零.已知sin15°=0.26,cos15°=0.97,tan30°=0.58,g=10m/s2.则汽车匀加速启动的加速度可能为( )
如图是汽车运送圆柱形工件的示意图.图中P、Q、N是固定在车体上的压力传感器,假设圆柱形工件表面光滑,汽车静止在水平地面上不动时Q传感器示数为零,P、N传感器示数不为零.现该汽车正沿倾角为15°的斜面向上匀加速启动,P传感器示数为零而Q、N传感器示数不为零.已知sin15°=0.26,cos15°=0.97,tan30°=0.58,g=10m/s2.则汽车匀加速启动的加速度可能为( )
 如图是汽车运送圆柱形工件的示意图.图中P、Q、N是固定在车体上的压力传感器,假设圆柱形工件表面光滑,汽车静止在水平地面上不动时Q传感器示数为零,P、N传感器示数不为零.现该汽车正沿倾角为15°的斜面向上匀加速启动,P传感器示数为零而Q、N传感器示数不为零.已知sin15°=0.26,cos15°=0.97,tan30°=0.58,g=10m/s2.则汽车匀加速启动的加速度可能为( )
如图是汽车运送圆柱形工件的示意图.图中P、Q、N是固定在车体上的压力传感器,假设圆柱形工件表面光滑,汽车静止在水平地面上不动时Q传感器示数为零,P、N传感器示数不为零.现该汽车正沿倾角为15°的斜面向上匀加速启动,P传感器示数为零而Q、N传感器示数不为零.已知sin15°=0.26,cos15°=0.97,tan30°=0.58,g=10m/s2.则汽车匀加速启动的加速度可能为( )| A. | 2m/s2 | B. | 3m/s2 | C. | 4m/s2 | D. | 5m/s2 |
15.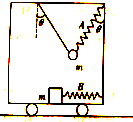 如图所示,沿水平面运动的小车里有用轻质细线和轻质弹簧A共同悬挂的小球,小车光滑底板上有用轻质弹簧B拴着的物块,已知悬线和轻质弹簧A与竖直方向夹角均为θ=30°,弹簧B处于压缩状态,小球和物块质量均为m,均相对小车静止,重力加速度为g,则( )
如图所示,沿水平面运动的小车里有用轻质细线和轻质弹簧A共同悬挂的小球,小车光滑底板上有用轻质弹簧B拴着的物块,已知悬线和轻质弹簧A与竖直方向夹角均为θ=30°,弹簧B处于压缩状态,小球和物块质量均为m,均相对小车静止,重力加速度为g,则( )
 如图所示,沿水平面运动的小车里有用轻质细线和轻质弹簧A共同悬挂的小球,小车光滑底板上有用轻质弹簧B拴着的物块,已知悬线和轻质弹簧A与竖直方向夹角均为θ=30°,弹簧B处于压缩状态,小球和物块质量均为m,均相对小车静止,重力加速度为g,则( )
如图所示,沿水平面运动的小车里有用轻质细线和轻质弹簧A共同悬挂的小球,小车光滑底板上有用轻质弹簧B拴着的物块,已知悬线和轻质弹簧A与竖直方向夹角均为θ=30°,弹簧B处于压缩状态,小球和物块质量均为m,均相对小车静止,重力加速度为g,则( )| A. | 小车一定水平向左做匀加速运动 | B. | 弹簧A一定处于拉伸状态 | ||
| C. | 弹簧B的弹力大小可能为$\frac{\sqrt{3}}{3}$mg | D. | 细线拉力有可能大于弹簧B的拉力 |
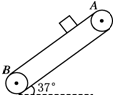 如图所示,传送带与地面倾角θ=37°,从A到B长度为16m,传送带以10m/s的速度转动.在传送带上端A处由静止放一个质量为2kg的小煤块,它与传送带之间的动摩擦因数为0.5.(sin 37°=0.6,cos 37°=0.8,g取10m/s2)则当皮带轮处于下列情况时,
如图所示,传送带与地面倾角θ=37°,从A到B长度为16m,传送带以10m/s的速度转动.在传送带上端A处由静止放一个质量为2kg的小煤块,它与传送带之间的动摩擦因数为0.5.(sin 37°=0.6,cos 37°=0.8,g取10m/s2)则当皮带轮处于下列情况时,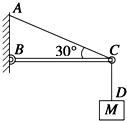 如图所示横梁BC为水平轻杆,且B端用铰链固定在竖直墙上,轻绳AD拴接在C端,D端所挂物体质量M=10kg,g取10m/s2,求:
如图所示横梁BC为水平轻杆,且B端用铰链固定在竖直墙上,轻绳AD拴接在C端,D端所挂物体质量M=10kg,g取10m/s2,求: