题目内容
1. 一束电子(不计重力)电子电荷量为e质量为m从静止开始经加速电压U1加速后,以水平速度射入水平放置的两平行金属板中间,如图所示,金属板长l,两板距离为d,竖直放置的荧光屏距金属板右端为L,若在两金属板间加直流电压U2时,光点偏离中线打在荧光屏上的P点,求:
一束电子(不计重力)电子电荷量为e质量为m从静止开始经加速电压U1加速后,以水平速度射入水平放置的两平行金属板中间,如图所示,金属板长l,两板距离为d,竖直放置的荧光屏距金属板右端为L,若在两金属板间加直流电压U2时,光点偏离中线打在荧光屏上的P点,求:(1)电子刚从加速电场出来时的速度v0;
(2)电子通过偏转电场的偏移量y;
(3)光点P距离O点的距离SOP.
分析 (1)根据动能定理求出电子刚从加速电场出来时的速度.
(2)根据牛顿第二定律和运动学公式,抓住等时性,求出电子通过偏转电场时的偏转位移.
(3)抓住粒子出偏转电场时速度反向延长线经过偏转电场中轴线的中点,根据相似三角形求出光点P距离O点的距离SOP.
解答 解:(1)根据动能定理得,$e{U}_{1}=\frac{1}{2}m{{v}_{0}}^{2}$,
解得${v}_{0}=\sqrt{\frac{2e{U}_{1}}{m}}$.
(2)电子的偏转位移y=$\frac{1}{2}a{t}^{2}=\frac{1}{2}\frac{e{U}_{2}}{md}\frac{{l}^{2}}{{{v}_{0}}^{2}}=\frac{{U}_{2}l}{2{U}_{1}d}$.
(3)因为粒子出电场时速度的反向延长线经过偏转电场中轴线的中点,根据相似三角形得,
$\frac{y}{{S}_{op}}=\frac{\frac{l}{2}}{\frac{l}{2}+L}$,
解得Sop=$\frac{{U}_{2}}{{U}_{1}d}(\frac{l}{2}+L)$.
答:(1)电子刚从加速电场出来时的速度为$\sqrt{\frac{2e{U}_{1}}{m}}$;
(2)电子通过偏转电场的偏移量y为$\frac{{U}_{2}l}{2{U}_{1}d}$;
(3)光点P距离O点的距离为$\frac{{U}_{2}}{{U}_{1}d}(\frac{l}{2}+L)$.
点评 本题考查了带电粒子在电场中的加速和偏转,知道粒子出电场后做匀速直线运动,对于第三问,也可以求出电子离开电场时的速度方向,根据几何关系进行求解.

练习册系列答案
相关题目
11. 如图所示,电梯的顶部挂有一个弹簧秤,秤下端挂了一个重物,电梯匀速直线运动时,弹簧秤的示数为l0N,在某时刻电梯中的人观察到弹簧秤的示数变为8N,关于电梯的运动,以下说法正确的是( )
如图所示,电梯的顶部挂有一个弹簧秤,秤下端挂了一个重物,电梯匀速直线运动时,弹簧秤的示数为l0N,在某时刻电梯中的人观察到弹簧秤的示数变为8N,关于电梯的运动,以下说法正确的是( )
 如图所示,电梯的顶部挂有一个弹簧秤,秤下端挂了一个重物,电梯匀速直线运动时,弹簧秤的示数为l0N,在某时刻电梯中的人观察到弹簧秤的示数变为8N,关于电梯的运动,以下说法正确的是( )
如图所示,电梯的顶部挂有一个弹簧秤,秤下端挂了一个重物,电梯匀速直线运动时,弹簧秤的示数为l0N,在某时刻电梯中的人观察到弹簧秤的示数变为8N,关于电梯的运动,以下说法正确的是( )| A. | 电梯可能向上加速运动,加速度大小为2m/s2 | |
| B. | 电梯可能向下加速运动,加速度大小为4m/s2 | |
| C. | 电梯可能向上减速运动,加速度大小为2m/s2 | |
| D. | 电梯可能向下减速运动,加速度大小为4m/s2 |
6.一个带正电的质点,电荷量q=3.0×10-5C,在静电场中由a点移到b点,在这过程中,除电场力外,其他力作的功为9.0×10-5J,质点的动能增加了1.5×10-4J则a、b两点间的电势差为( )
| A. | 3V | B. | 2 V | C. | 5V | D. | 8 V |
10. 如图所示,A、B两物体的重力分别是GA=3N,GB=4N.A用细线悬挂在顶板上,B放在水平面上,A、B间轻弹簧中的弹力F=2N,则细线中的张力T及B对地面的压力N的可能值分别是( )
如图所示,A、B两物体的重力分别是GA=3N,GB=4N.A用细线悬挂在顶板上,B放在水平面上,A、B间轻弹簧中的弹力F=2N,则细线中的张力T及B对地面的压力N的可能值分别是( )
 如图所示,A、B两物体的重力分别是GA=3N,GB=4N.A用细线悬挂在顶板上,B放在水平面上,A、B间轻弹簧中的弹力F=2N,则细线中的张力T及B对地面的压力N的可能值分别是( )
如图所示,A、B两物体的重力分别是GA=3N,GB=4N.A用细线悬挂在顶板上,B放在水平面上,A、B间轻弹簧中的弹力F=2N,则细线中的张力T及B对地面的压力N的可能值分别是( )| A. | 5 N和6 N | B. | 5 N和2 N | C. | 1 N和6 N | D. | 1 N和2 N |
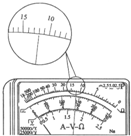 某人用多用电表按正确步骤测量一个电阻的阻值,当选择欧姆挡“×1”挡测量时,指针指示位置如图所示,则其电阻值是12.如果要用这支多用电表测量一个约200欧的电阻,为了使测量比较精确,选择开关应选的欧姆挡是×10.(填“×1”、“×10”或“×100”).
某人用多用电表按正确步骤测量一个电阻的阻值,当选择欧姆挡“×1”挡测量时,指针指示位置如图所示,则其电阻值是12.如果要用这支多用电表测量一个约200欧的电阻,为了使测量比较精确,选择开关应选的欧姆挡是×10.(填“×1”、“×10”或“×100”).