题目内容
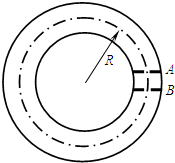 (2011?河东区一模)如图所示为一种获得高能粒子的装置.环形区域内存在垂直直面向外、大小可调的匀强磁场,质量为m、电荷量为+q的粒子,在环中做半径为R的圆周运动,A、B为两块中心开有小孔的极板,原来电势均为零,每当粒子飞经A板时,A板电势升高为+U,B板电势仍保持为零,粒子在两极中得到加速.每当粒子离开时,A极电势又降为零,粒子在电场中一次一次加速下动能不断增大,而绕行半径不变.
(2011?河东区一模)如图所示为一种获得高能粒子的装置.环形区域内存在垂直直面向外、大小可调的匀强磁场,质量为m、电荷量为+q的粒子,在环中做半径为R的圆周运动,A、B为两块中心开有小孔的极板,原来电势均为零,每当粒子飞经A板时,A板电势升高为+U,B板电势仍保持为零,粒子在两极中得到加速.每当粒子离开时,A极电势又降为零,粒子在电场中一次一次加速下动能不断增大,而绕行半径不变.(1)设t=0时,粒子静止在A板小孔处,在电场作用下加速,并开始绕行第一圈,求粒子绕行n圈回到A板时获得的动能En;
(2)为使粒子运动半径始终不变,磁场必周期性递增,求粒子绕行第n圈时磁感应强度Bn为多少?
(3)求粒子绕行n圈所需的总时间tn.(设极板间距远小于R)
分析:(1)由题意可知,每加速一次,粒子的能量就增加qU,所以绕行n圈时粒子的总动能为nqU.
(2)能量逐渐增加,速度就逐渐增加,由能量可表示出速度,洛伦兹力提供向心力,由牛顿第二定律即可求出第n圈时的磁场强度.
(3)每圈的半径没有发生变化,由周长和每圈的速度即可求出每圈的时间,然后相累加.
(2)能量逐渐增加,速度就逐渐增加,由能量可表示出速度,洛伦兹力提供向心力,由牛顿第二定律即可求出第n圈时的磁场强度.
(3)每圈的半径没有发生变化,由周长和每圈的速度即可求出每圈的时间,然后相累加.
解答:解:
(1)粒子绕行一圈,动能的增量为qU,则绕行n圈所获得的总动能为:
En=nqU
(2)因为有:nqU=
m
qvnBn=m
得:Bn=
(3)粒子做半径为R的匀速圆周运动,每一圈所用的时间为
,由于每一圈速度不同,所以每一圈所所需时间也不同,
第一圈:
qU=
m
v1=
第二圈:
2qU=
m
v2=
…
第n圈的速度为:
vn=
故绕行n圈所用的时间为:
t=t1+t2+…+tn
=
+
+…+
=2πR
(1+
+
+…+
)
答:(1)粒子绕行n圈回到A板时获得的动能为nqU
(2)粒子绕行第n圈时磁感应强度为
(3)求粒子绕行n圈所需的总时间为2πR
(1+
+
+…+
).
(1)粒子绕行一圈,动能的增量为qU,则绕行n圈所获得的总动能为:
En=nqU
(2)因为有:nqU=
| 1 |
| 2 |
| v | 2 n |
qvnBn=m
| ||
| R |
得:Bn=
| 1 |
| R |
|
(3)粒子做半径为R的匀速圆周运动,每一圈所用的时间为
| 2πR |
| v |
第一圈:
qU=
| 1 |
| 2 |
| v | 2 1 |
v1=
|
第二圈:
2qU=
| 1 |
| 2 |
| v | 2 2 |
v2=
|
…
第n圈的速度为:
vn=
|
故绕行n圈所用的时间为:
t=t1+t2+…+tn
=
| 2πR |
| v1 |
| 2πR |
| v2 |
| 2πR |
| vn |
=2πR
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
答:(1)粒子绕行n圈回到A板时获得的动能为nqU
(2)粒子绕行第n圈时磁感应强度为
| 1 |
| R |
|
(3)求粒子绕行n圈所需的总时间为2πR
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
点评:粒子加速器是利用磁场的偏转使电场能重复对粒子加速,粒子在加速器内旋转时半径是不变化的,所以粒子加速器所加的磁场时要发生变.速度越来越大,周期越来越小.解决此类问题,常用到能量的转化与守恒,粒子在匀强磁场中的运动半径和周期.对于周期的计算也可以用圆周的长度除以速度.

练习册系列答案
相关题目
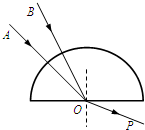 (2011?河东区一模)如图所示,两束单色光A、B分别沿半径方向由空气射入半圆形玻璃砖,出射光合成一束复色光P,下列说法中正确的是( )
(2011?河东区一模)如图所示,两束单色光A、B分别沿半径方向由空气射入半圆形玻璃砖,出射光合成一束复色光P,下列说法中正确的是( )
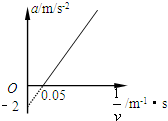 (2011?河东区一模)(1)一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数(1/v)图象如图所示.若已知汽车的质量为m=1.5×103kg,则汽车运行时的功率为
(2011?河东区一模)(1)一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数(1/v)图象如图所示.若已知汽车的质量为m=1.5×103kg,则汽车运行时的功率为