题目内容
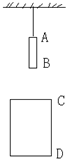
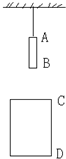 如图所示,悬挂着的一根长为15m的直杆AB,在直杆正下方5m处有一个无底圆筒CD.若将悬线剪短,直杆通过圆筒所用的时间为2s,求无底圆筒的长度.
如图所示,悬挂着的一根长为15m的直杆AB,在直杆正下方5m处有一个无底圆筒CD.若将悬线剪短,直杆通过圆筒所用的时间为2s,求无底圆筒的长度.
解:取杆的下端B点为研究对象,
设下降5m时B点的速度的大小为v,
根据v2=2gh可得,
v=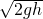 =
= m/s=10m/s,
m/s=10m/s,
直杆通过圆筒的时间是从B点进入圆筒开始,到A点离开圆筒时结束,
设圆筒的长度为l,则在2s内杆下降的距离为l+15,
由位移公式可得,l+15=vt+ gt2,
gt2,
即 l+15=10×2+ ×10×22,
×10×22,
解得 l=25m,
答:无底圆筒的长度为25m.
分析:直杆做的是自由落体运动,根据自由落体运动的规律可以求得下降5m时杆的速度的大小,再由位移公式可以求得在2s内杆下降的距离,此距离即为杆和圆筒的总长度的大小,
点评:解决本题的关键的地方是找出杆通过圆筒时位移的关系,杆通过圆筒是从B点进入圆筒开始的,到A点离开圆筒时结束,此时下降的位移为杆和圆筒长度的和.
设下降5m时B点的速度的大小为v,
根据v2=2gh可得,
v=
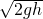 =
= m/s=10m/s,
m/s=10m/s,直杆通过圆筒的时间是从B点进入圆筒开始,到A点离开圆筒时结束,
设圆筒的长度为l,则在2s内杆下降的距离为l+15,
由位移公式可得,l+15=vt+
 gt2,
gt2,即 l+15=10×2+
 ×10×22,
×10×22,解得 l=25m,
答:无底圆筒的长度为25m.
分析:直杆做的是自由落体运动,根据自由落体运动的规律可以求得下降5m时杆的速度的大小,再由位移公式可以求得在2s内杆下降的距离,此距离即为杆和圆筒的总长度的大小,
点评:解决本题的关键的地方是找出杆通过圆筒时位移的关系,杆通过圆筒是从B点进入圆筒开始的,到A点离开圆筒时结束,此时下降的位移为杆和圆筒长度的和.

练习册系列答案
相关题目
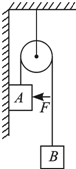 如图所示,跨过定滑轮的细绳的两端悬挂着重物A和B,当用一水平力F将A压在竖直墙上时,悬挂A的绳恰好竖直.已知物体A重GA=10N,A与墙之间的动摩擦因数μ=0.4,水平压力F=5N.要使物体匀速下滑,物体B的重力应为多大?(不计细绳的质量及滑轮的摩擦)
如图所示,跨过定滑轮的细绳的两端悬挂着重物A和B,当用一水平力F将A压在竖直墙上时,悬挂A的绳恰好竖直.已知物体A重GA=10N,A与墙之间的动摩擦因数μ=0.4,水平压力F=5N.要使物体匀速下滑,物体B的重力应为多大?(不计细绳的质量及滑轮的摩擦) 如图所示,悬挂着的一根长为15m的直杆AB,在直杆正下方5m处有一个无底圆筒CD.若将悬线剪短,直杆通过圆筒所用的时间为2s,求无底圆筒的长度.
如图所示,悬挂着的一根长为15m的直杆AB,在直杆正下方5m处有一个无底圆筒CD.若将悬线剪短,直杆通过圆筒所用的时间为2s,求无底圆筒的长度.