题目内容
11.某人在距地面2m高处,将质量为2kg的小球以3m/s的速度水平抛出(取g=10m/s2).(1)若不计空气阻力,求小球落地时速度的大小;
(2)若小球落地时速度大小是5m/s,求小球在空中克服阻力所做的功.
分析 根据动能定理求出人抛球做功的大小,对抛出到落地过程研究,运用动能定理求出小球落地时的速度,以及通过动能定理求出小球在空中克服阻力做功的大小.
解答 解:(1)根据动能定理得,mgh=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$
解得$v=\sqrt{{{v}_{0}}^{2}+2gh}=\sqrt{9+20×2}m/s=7m/s$.
(2)根据动能定理得,
mgh-${W}_{f}=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$
解得Wf=24J.
答:(1)不计空气阻力,小球落地时速度的大小7m/s
(2)小球在空中克服阻力做功为24J.
点评 本题考查了动能定理的基本运用,运用动能定理解题,首先确定研究的过程,判断该过程中有哪些力做功,通过动能定理列式求解.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
1.在“验证机械能守恒定律”实验中,在下面所列举的该实验的几个操作步骤中,你认为没有必要进行的或者错误的步骤是( )
| A. | 按照图示的装置安装器件 | |
| B. | 将打点计时器接到学生电源的直流输出端上 | |
| C. | 用天平测量出重物的质量 | |
| D. | 先放手让纸带和重物下落,再接通电源开关 | |
| E. | 在打出的纸带上,依据打点的先后顺序选取A、B、C、D(如图所示)四个合适的相邻点,通过测量计算得出B、C两点的速度为vB、vC,并测出B、C两点间的距离为h | |
| F. | 在误差允许范围内,看减少的重力势能mgh是否等于增加的动能$\frac{1}{2}$mv${\;}_{C}^{2}$-$\frac{1}{2}$mv${\;}_{B}^{2}$,从而验证机械能守恒定律 |
2. 2009年5月,航天飞机在完成对哈勃空间望远镜的维修任务后,在A点从圆形轨道Ⅰ进入椭圆轨道Ⅱ,B为轨道Ⅱ上的一点,如图所示,关于航天飞机的运动,下列说法中正确的有( )
2009年5月,航天飞机在完成对哈勃空间望远镜的维修任务后,在A点从圆形轨道Ⅰ进入椭圆轨道Ⅱ,B为轨道Ⅱ上的一点,如图所示,关于航天飞机的运动,下列说法中正确的有( )
 2009年5月,航天飞机在完成对哈勃空间望远镜的维修任务后,在A点从圆形轨道Ⅰ进入椭圆轨道Ⅱ,B为轨道Ⅱ上的一点,如图所示,关于航天飞机的运动,下列说法中正确的有( )
2009年5月,航天飞机在完成对哈勃空间望远镜的维修任务后,在A点从圆形轨道Ⅰ进入椭圆轨道Ⅱ,B为轨道Ⅱ上的一点,如图所示,关于航天飞机的运动,下列说法中正确的有( )| A. | 在轨道Ⅱ上经过A的速度等于经过B的速度 | |
| B. | 在轨道Ⅱ上经过A的动能大于在轨道Ⅰ上经过A 的动能 | |
| C. | 在轨道Ⅱ上运动的周期小于在轨道Ⅰ上运动的周期 | |
| D. | 在轨道Ⅱ上经过A的加速度等于在轨道Ⅰ上经过A的加速度 |
19.平行板电容器A、B两板加上如图所示的交变电压,开始A板电势比B板高,这时两极板中间原来静止的电子在电场力作用下开始运动,设电子运动不与极板相碰,以下说法正确的是(不计电子的重力)( )


| A. | 先向A运动,然后向B运动,再返回A板做周期性来回运动 | |
| B. | 一直向A板运动 | |
| C. | 一直向B板运动 | |
| D. | 先向B运动,然后向A运动,再返回B板做周期性来回运动 |
6. 如图,一轻绳的一端系在固定粗糙斜面上的O点,另一端系一小球,给小球一足够大的初速度,使小球在斜面上做圆周运动.在此过程中( )
如图,一轻绳的一端系在固定粗糙斜面上的O点,另一端系一小球,给小球一足够大的初速度,使小球在斜面上做圆周运动.在此过程中( )
 如图,一轻绳的一端系在固定粗糙斜面上的O点,另一端系一小球,给小球一足够大的初速度,使小球在斜面上做圆周运动.在此过程中( )
如图,一轻绳的一端系在固定粗糙斜面上的O点,另一端系一小球,给小球一足够大的初速度,使小球在斜面上做圆周运动.在此过程中( )| A. | 小球的机械能守恒 | |
| B. | 重力对小球做正功 | |
| C. | 绳的拉力对小球不做功 | |
| D. | 在任何一段时间内,小球克服摩擦力所做的功总是等于小球动能的减少 |
16.如图为“验证机械能守恒定律”的实验装置,下列哪些说法是正确的( )
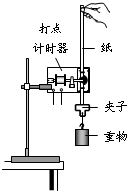

| A. | 实验时应选用密度大体积小,并且下端有橡胶垫的重锤 | |
| B. | 实验时,当松开纸带让重锤下落同时,立即接通电源 | |
| C. | 要选用第1、2点间距离接近2mm的纸带 | |
| D. | 实验结果总是动能的增量略大于重力势能的减小量 |
3.对于跳伞运动员在刚跳离飞机,其降落伞尚未打开的一段时间内,下列说法中错误的是( )
| A. | 空气阻力做正功 | B. | 重力做正功 | C. | 合外力做正功 | D. | 空气阻力做负功 |
 电站发电机端电压u=5000$\sqrt{2}$sin314tV,输出功率5000kW,远距离输电线的电阻为80Ω,输电线上功率损耗要求不超过总功率的4%,则
电站发电机端电压u=5000$\sqrt{2}$sin314tV,输出功率5000kW,远距离输电线的电阻为80Ω,输电线上功率损耗要求不超过总功率的4%,则