题目内容
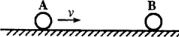[选做题]如图所示，光滑水平面上有两个大小相同的钢球A、B，A球的质量大于B球的质量，开始时A球以一定的速度向右运动，B球处于静止状态．两球碰撞后均向右运动．设碰撞前A球的德布罗意波长为λ1，碰撞后A、B两球的德布罗意波长分别为λ2和λ3．已知运动物体的德布罗意波长和动量之间的关系式为，λ=| h |
| p |
分析：在光滑水平面上，大小虽然相同，但质量不等．在碰撞过程中系统满足动量守恒定律，因此可以利用运动物体的德布罗意波长和动量之间的关系列出动量守恒表达式，从而求出结果．
解答：解：如图所示．球A、B碰撞过程中，满足动量守恒．则PB′-0=PA-PA′
由λ=
，可得P=
即动量守恒表达式也可写成：
=
-
所以λ1=
故选：C
．球A、B碰撞过程中，满足动量守恒．则PB′-0=PA-PA′由λ=
| h |
| p |
| h |
| λ |
即动量守恒表达式也可写成：
| h |
| λ3 |
| h |
| λ1 |
| h |
| λ2 |
所以λ1=
| λ3λ2 |
| λ3+λ2 |
故选：C
点评：动量守恒定律表达式具有矢量性，因此列式时须确定正方向．
练习册系列答案
相关题目
（选做题）如图所示，在A、B两点间接一电动势为4V，内电阻为1Ω的直流电源，电阻R1、R2、R3的阻值均为4Ω，电容器的电容为30μF，电流表的内阻不计，当电键S闭合时，求：（1）电流表的读数；（2）电容器所带的电量；（3）断开电键S后，通过R2的电量．
（选做题）如图所示电路，变阻器R1的最大值为4Ω，此时它的有效电阻为2Ω，定值电阻R2=6Ω，电源内阻r=1Ω．当开关闭合时，电源消耗的总功率为16W，输出功率为12W，这时灯正常发光．求：（1）电灯的电阻；（2）当开关断开时，要使灯仍能正常发光，求出此时电源的输出功率和电源的效率？
【选做题】如图所示，在平面直角坐标系xoy中，第一象限存在沿y轴负方向的匀强电场，第四象限存在垂直纸面向外的匀强磁场，磁感应强度B=
