题目内容
【题目】在行星绕太阳的椭圆运动中,若令![]() ,
,![]() ,其中,
,其中,![]() 为周期,
为周期,![]() 为半长轴,
为半长轴,![]() 为离心率.在天文学上,称
为离心率.在天文学上,称![]() 为偏近点角,试证开普勒方程:
为偏近点角,试证开普勒方程:![]() .(当行星处子近日点时,取
.(当行星处子近日点时,取![]() ,即
,即![]() )注:偏近点角是过椭圆上的任意一点,垂直于椭圆半长轴,交半长轴外接圆的点到原点的直线与半长轴所成夹角.在椭圆的参数方程
)注:偏近点角是过椭圆上的任意一点,垂直于椭圆半长轴,交半长轴外接圆的点到原点的直线与半长轴所成夹角.在椭圆的参数方程![]() ,
,![]() 中,参数角
中,参数角![]() 即为偏近点角
即为偏近点角
【答案】证明见解析
【解析】
方法1:由能量关系,得![]()
则![]() . ①
. ①
由于![]() ,则
,则![]() .
.
由于![]() ,其中
,其中![]() ,则
,则![]() .
.
由于![]() ,则
,则
![]() , ②
, ②
![]()
则![]() , ③
, ③
![]() . ④
. ④
把③④代入①,得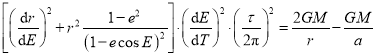 .
.
代入②,得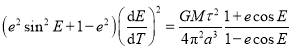 .
.
由开普勒第三定律,得![]() ,则
,则![]() .
.
积分,得![]() .
.
由于处于近点时,![]() ,而此时
,而此时![]() ,得
,得![]() ,则
,则![]() ,
,
即![]() .
.
方法2:建立如图所示的坐标系,则轨道方程为
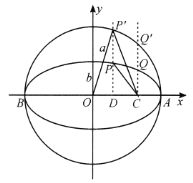
![]() .
.
同时,![]() ,
,![]() .
.
对于任意一点![]() ,有
,有![]() ,
,
而![]() ,则
,则![]() .
.
为此,作以![]() 为圆心,以
为圆心,以![]() 为半径的圆,方程为
为半径的圆,方程为![]() .
.
过![]() 作
作![]() 轴平行线交圆于
轴平行线交圆于![]() ,则
,则![]() ,
,![]() .
.
![]() 为从近日点到任意点
为从近日点到任意点![]() 的时间,其间转过了
的时间,其间转过了![]() 圈,则
圈,则![]() .
.
![]() 为面积速度,
为面积速度,![]() ,关键是求
,关键是求![]() ,由于对于同样的
,由于对于同样的![]() ,椭圆、圆上对应的纵坐标
,椭圆、圆上对应的纵坐标![]() 、
、![]() ,易知
,易知![]() ,则
,则![]() ,则
,则![]() .
.
又![]() ,
,
![]() .
.
则![]() ,
,
则![]() ,
,
则![]() ,
,
则![]() .
.
上面计算中,![]() 只取了
只取了![]() 中的一个值,故只需再推广
中的一个值,故只需再推广![]() 的定义,上式即化为
的定义,上式即化为![]() .
.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目