题目内容
14.某同学这样来推导地球第一宇宙速度:v≈$\frac{2πR}{T}$=$\frac{2×3.14×6.4×1{0}^{6}}{24×3600}$m/s≈465m/s,其结果与正确值相差很远,这是由于他在近似处理中,错误地假设( )| A. | 卫星沿圆轨道运动 | |
| B. | 卫星所需的向心力等于地球对它的引力 | |
| C. | 卫星轨道半径等于地球半径 | |
| D. | 卫星的周期等于地球自转的周期 |
分析 第一宇宙速度(又称环绕速度),是指物体紧贴地球表面作圆周运动的速度,所以有两个条件:卫星做匀速圆周运动;卫星的轨道半径等于地球半径.根据万有引力提供向心力,列出表达式即可求解.
解答 解:第一宇宙速度(又称环绕速度):是指物体紧贴地球表面作圆周运动的速度(也是人造地球卫星的最小发射速度).所以做出的假设有两个:(1)卫星做匀速圆周运动;(2)贴近地面,即:卫星的轨道半径等于地球半径.
计算方法是:$\frac{GMm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$,其中:M是地球的质量,R是地球的半径,得:v=$\sqrt{\frac{GM}{R}}$.故A、B、C正确,D错误
本题选错误的,故选:D.
点评 此题需明确第一宇宙速度计算方法是:$\frac{GMm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$,得:v=$\sqrt{\frac{GM}{R}}$.围绕原理可找出需要做出的假设.

练习册系列答案
相关题目
4.一列沿x轴正方向传播的简谐机械横波,波速为2m/s.某时刻波形如图所示,下列说法正确的是( )
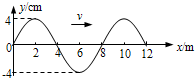

| A. | 这列波的周期为2s | B. | 这列波的振幅为8cm | ||
| C. | 此时x=8m处质点沿y轴负方向运动 | D. | 此时x=4m处质点的速度大小为零 |
5.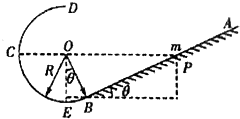 如图所示,AB是倾角θ=37°的粗糙直轨道,BCD是光滑圆弧轨道,AB恰好在B点与圆轨相切,圆轨半径R=4m.现将质量为m=5kg的小物体从直轨道上的P点由静止释放,最终它将在圆轨上往复运动.已知P点与圆轨圆心O等高,物体与轨道AB间的动摩擦因数为μ=0.2,g取10m/s2,sin37°=0.6,cos37°=0.8.则下列有关说法正确的是( )
如图所示,AB是倾角θ=37°的粗糙直轨道,BCD是光滑圆弧轨道,AB恰好在B点与圆轨相切,圆轨半径R=4m.现将质量为m=5kg的小物体从直轨道上的P点由静止释放,最终它将在圆轨上往复运动.已知P点与圆轨圆心O等高,物体与轨道AB间的动摩擦因数为μ=0.2,g取10m/s2,sin37°=0.6,cos37°=0.8.则下列有关说法正确的是( )
 如图所示,AB是倾角θ=37°的粗糙直轨道,BCD是光滑圆弧轨道,AB恰好在B点与圆轨相切,圆轨半径R=4m.现将质量为m=5kg的小物体从直轨道上的P点由静止释放,最终它将在圆轨上往复运动.已知P点与圆轨圆心O等高,物体与轨道AB间的动摩擦因数为μ=0.2,g取10m/s2,sin37°=0.6,cos37°=0.8.则下列有关说法正确的是( )
如图所示,AB是倾角θ=37°的粗糙直轨道,BCD是光滑圆弧轨道,AB恰好在B点与圆轨相切,圆轨半径R=4m.现将质量为m=5kg的小物体从直轨道上的P点由静止释放,最终它将在圆轨上往复运动.已知P点与圆轨圆心O等高,物体与轨道AB间的动摩擦因数为μ=0.2,g取10m/s2,sin37°=0.6,cos37°=0.8.则下列有关说法正确的是( )| A. | 物体从释放到最终做往复运动,在AB轨道通过的总路程为25m | |
| B. | 物体从释放到最终做往复运动,物体克服摩擦力做功为160J | |
| C. | 最终做往复运动时,物体对轨道最低点E压力大小为70N | |
| D. | 要使物体能顺利到达圆弧轨道最高点D,释放点距离E点高度差为8m |
2.由于地球的自转,使得静止在赤道地面的物体绕地轴做匀速圆周运动.对于这些做匀速圆周运动的物体,以下说法正确的是( )
| A. | 向心力都指向地心 | B. | 速度等于第一宇宙速度 | ||
| C. | 加速度等于重力加速度 | D. | 周期与地球自转的周期相等 |
9.下列不属于预防静电危害的做法是( )
| A. | 在高大的建筑物顶端安装避雷针 | |
| B. | 水泥厂利用静电除去废气中的粉尘 | |
| C. | 在制造轮胎的橡胶中添加导电材料 | |
| D. | 行驶中的油罐车尾带一条拖地的铁链 |
6.关于竖直下抛运动,下列说法中正确的是( )
| A. | 和自由落体运动运动一样初速度向下 | |
| B. | 除受重力作用外,还受到下抛力的作用 | |
| C. | 属于变加速直线运动 | |
| D. | 可看作是自由落体运动和竖直向下匀速直线运动的合运动 |
3.地球同步卫星质量为m,离地高度为h,若地球半径为R0,地球表面处重力加速度为g0,地球自转角速度为ω0,则同步卫星所受的地球对它的万有引力的大小为 ( )
| A. | 0 | B. | mg0$\frac{{R}_{0}}{({R}_{0}+h)^{2}}$ | C. | mω02(R0+h) | D. | mω$\root{3}{{R}_{0}{{g}_{0}}^{2}{{ω}_{0}}^{4}}$ |
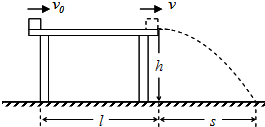 如图所示,质量为m的可视为质点的小物块在粗糙水平桌面上做直线运动,经距离l后以速度v飞离桌面,最终落在水平地面上.已知l=1.4m,v=3.0m/s,m=0.10kg,物块与桌面间的动摩擦因数?=0.25,桌面高h=0.45m.不计空气阻力,重力加速度取10m/s2.求:
如图所示,质量为m的可视为质点的小物块在粗糙水平桌面上做直线运动,经距离l后以速度v飞离桌面,最终落在水平地面上.已知l=1.4m,v=3.0m/s,m=0.10kg,物块与桌面间的动摩擦因数?=0.25,桌面高h=0.45m.不计空气阻力,重力加速度取10m/s2.求: