题目内容
11. 如图所示,在光滑水平面上使滑块A以2m/s的速度向右运动,滑块B以4m/s的速度向左运动并与滑块A发生碰撞,已知滑块A、B的质量分别为1kg、2kg,滑块B的左侧连有轻弹簧,求:
如图所示,在光滑水平面上使滑块A以2m/s的速度向右运动,滑块B以4m/s的速度向左运动并与滑块A发生碰撞,已知滑块A、B的质量分别为1kg、2kg,滑块B的左侧连有轻弹簧,求:(1)当滑块A的速度减为0时,滑块B的速度大小;
(2)弹簧的最大弹性势能.
分析 (1)对于A、B构成的系统,在A压缩弹簧过程中,系统的合外力为零,满足动量守恒,根据动量守恒定律求解即可.
(3)当两个物体的速度相等时,弹簧压缩最短,弹性势能最大,根据系统的机械能列式求解
解答 解:(1)系统动量守恒,以向右为正方向,
由动量守恒定律得:mAv1-mBv2=mBv3,
1×2-2×4=2×v3,
解得:v3=-3m/s,方向:水平向左;
(2)当A、B速度相同时弹簧的弹性势能最大,
以向右为正方向,由动量守恒定律得:
mAv1-mBv2=(mA+mB)v,即:1×2-2×4=(1+2)v,
由能量守恒定律得:EP=$\frac{1}{2}$mAv12+$\frac{1}{2}$mBv22-$\frac{1}{2}$(mA+mB)v2,
EP=$\frac{1}{2}$×1×22+$\frac{1}{2}$×2×42-$\frac{1}{2}$×(1+2)v2,
解得,最大的弹性势能:EP=4.5J;
答:(1)当滑块A的速度减为0时,滑块B的速度大小为3m/s;
(2)弹簧的最大弹性势能为4.5J.
点评 本题考查了求速度与弹性势能,分析清楚物体运动过程是正确解题的关键,应用动量守恒定律与能量守恒定律即可解题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
19.在研究大气现象时可把温度、压强相同的一部分气体叫做气团,气团可看做理想气体作为研究对象.气团直径很大可达几千米,其边缘部分与外界的热交换相对于整个气团的内能来说非常小,可以忽略不计.气团从地面上升到高空后温度可降低到-50℃,关于气团上升过程中下列说法不正确的是 ( )
| A. | 气团体积膨胀,对外做功,内能增大,压强减少 | |
| B. | 气团体积收缩,外界对气团做功,内能减少,压强增大 | |
| C. | 气团体积膨胀,对外做功,内能减少,压强减少 | |
| D. | 气团体积收缩,外界对气团做功,内能增大,压强不变 |
6.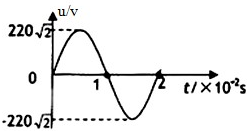 某交流发电机的输出电压随时间变化的关系,采用远距离输电如图所示,某次输出功率是20kW,用5000V高压输电,输电线总电阻是10Ω,则下列说法正确的是( )
某交流发电机的输出电压随时间变化的关系,采用远距离输电如图所示,某次输出功率是20kW,用5000V高压输电,输电线总电阻是10Ω,则下列说法正确的是( )
 某交流发电机的输出电压随时间变化的关系,采用远距离输电如图所示,某次输出功率是20kW,用5000V高压输电,输电线总电阻是10Ω,则下列说法正确的是( )
某交流发电机的输出电压随时间变化的关系,采用远距离输电如图所示,某次输出功率是20kW,用5000V高压输电,输电线总电阻是10Ω,则下列说法正确的是( )| A. | 交变电流的频率为100 Hz | |
| B. | 发电机输出电压的有效值为220 V | |
| C. | 输电线中电流为500 A | |
| D. | 提高升压变压器的升压比(n2:n1),输电线路损耗将减小 |
16.A、B两个质点,分别做匀速圆周运动,在相等时间内它们通过的弧长比lA:lB=4:3,转过的圆心角比θA:θB=3:2.则下列说法中正确的是( )
| A. | 它们的线速度比vA:vB=3:4 | B. | 它们的角速度比ωA:ωB=2:3 | ||
| C. | 它们的周期比TA:TB=2:3 | D. | 它们的向心加速度比aA:aB=2:1 |
3. 如图所示,把一个架在绝缘支架上的枕形导体放在正电荷形成的电场中,导体处于静电平衡时,下叙说法正确的是( )
如图所示,把一个架在绝缘支架上的枕形导体放在正电荷形成的电场中,导体处于静电平衡时,下叙说法正确的是( )
 如图所示,把一个架在绝缘支架上的枕形导体放在正电荷形成的电场中,导体处于静电平衡时,下叙说法正确的是( )
如图所示,把一个架在绝缘支架上的枕形导体放在正电荷形成的电场中,导体处于静电平衡时,下叙说法正确的是( )| A. | A、B两点电场强度相等,电势相等 | |
| B. | A、B两点的电场强度不相等,电势相等 | |
| C. | 感应电荷产生的附加场强大小是|EA|<|EB| | |
| D. | 当电键K闭合时,电子沿导线移向大地 |
1.我国于2013年12月发射了“嫦娥三号”卫星,该卫星在距月球表面高度为h的轨道上做匀速圆周运动,其运行的周期为T;卫星还在月球上软着陆.若以R表示月球的半径,忽略月球自转及地球对卫星的影响.则( )
| A. | 月球的第一宇宙速度为$\frac{{2π\sqrt{R{{(R+h)}^3}}}}{TR}$ | |
| B. | 物体在月球表面自由下落的加速度大小为$\frac{{4{π^2}{{(R+h)}^3}}}{{{R^2}{T^2}}}$ | |
| C. | “嫦娥三号”绕月运行时的向心加速度为$\frac{{4{π^2}R}}{T^2}$ | |
| D. | “嫦娥三号”降落月球时,可以使用降落伞减速 |
 在用电火花计时器“研究匀变速直线运动”的实验中,如图所示是一次记录小车车运动情况的纸带,图中A、B、C、D、E为相邻的计数点,相邻计数点间还有四个点未画出.(电源频率为50Hz)
在用电火花计时器“研究匀变速直线运动”的实验中,如图所示是一次记录小车车运动情况的纸带,图中A、B、C、D、E为相邻的计数点,相邻计数点间还有四个点未画出.(电源频率为50Hz) 电场中A,B两点间的电势差U为100V,把带电量为q=1.6×10-2C的粒子,从电场中的A点移动到B点的过程中,求:
电场中A,B两点间的电势差U为100V,把带电量为q=1.6×10-2C的粒子,从电场中的A点移动到B点的过程中,求: