题目内容
13. 有一小船从A处渡河,如图所示,已知河宽为400m,其下游300m处是暗礁的危险水域,水流速度恒为5m/s,欲使小船能安全到达对岸.
有一小船从A处渡河,如图所示,已知河宽为400m,其下游300m处是暗礁的危险水域,水流速度恒为5m/s,欲使小船能安全到达对岸.(1)则船相对静水的最小速度应是多少?
(2)此时船头的指向与河岸的夹角又是多大.
分析 为了使小船在危险水域之前到达对岸,临界情况是小船到达危险水域前,恰好到达对岸,确定出合位移的方向,即为合速度的方向,根据合速度的方向和水流速度,根据平行四边形定则确定静水速的最小值.
解答  解:设小船到达危险水域前,恰好到达对岸,则其合位移方向如图所示,设合位移方向与河岸的夹角为α,则
解:设小船到达危险水域前,恰好到达对岸,则其合位移方向如图所示,设合位移方向与河岸的夹角为α,则
tan(90°-α)=$\frac{300}{400}$=0.75,
解得:α=53°
小船的合速度方向与合位移方向相同,根据平
行四边形定则知,当船相对于静水的速度 v1垂直于合速度时,v1最小,
由图可知,v1的最小值为v1min=v2sinα=5×$\frac{4}{5}$m/s=4m/s,
这时v1的方向与河岸的夹角β=90°-α=37°;
而在离对岸400m时,离其下游300m,则船头的指向与河岸的夹角为37°,即为小船船头的指向.
答:(1)则船相对静水的最小速度应是4m/s;
(2)此时船头的指向与河岸的夹角是37°.
点评 解决本题的关键知道位移、速度是矢量,合成分解遵循平行四边形定则,注意几何关系在题目中的正确运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.关于磁感应强度B,下列说法中正确的是( )
| A. | 磁场中某点B的大小,跟放在该点的试探电流元的情况有关 | |
| B. | 磁场中某点B的方向,跟该点处试探电流元所受磁场力方向一致 | |
| C. | 在磁场中某点试探电流元不受磁场力作用时,该点B值大小为零 | |
| D. | 在磁场中磁感线越密集的地方,B值越大 |
1.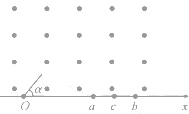 如图所示,在x轴上方有垂直于纸面向外的匀强磁场,两带正电且电量相同而质量不同的粒子A和B,已知A、B的质量分别为m1和m2,两粒子以相同的速率从O点以与x轴正方向成α=60°角垂直射入磁场,发现粒子A从a点射出磁场,粒子B从b点射出磁场.若另一与A、B带电量相同而质量不同的粒子C以相同速率与x轴正方向成α=30°角射入x轴上方时,发现它从ab的中点c射出磁场,则下列说法中正确的是(不计所有粒子重力)( )
如图所示,在x轴上方有垂直于纸面向外的匀强磁场,两带正电且电量相同而质量不同的粒子A和B,已知A、B的质量分别为m1和m2,两粒子以相同的速率从O点以与x轴正方向成α=60°角垂直射入磁场,发现粒子A从a点射出磁场,粒子B从b点射出磁场.若另一与A、B带电量相同而质量不同的粒子C以相同速率与x轴正方向成α=30°角射入x轴上方时,发现它从ab的中点c射出磁场,则下列说法中正确的是(不计所有粒子重力)( )
 如图所示,在x轴上方有垂直于纸面向外的匀强磁场,两带正电且电量相同而质量不同的粒子A和B,已知A、B的质量分别为m1和m2,两粒子以相同的速率从O点以与x轴正方向成α=60°角垂直射入磁场,发现粒子A从a点射出磁场,粒子B从b点射出磁场.若另一与A、B带电量相同而质量不同的粒子C以相同速率与x轴正方向成α=30°角射入x轴上方时,发现它从ab的中点c射出磁场,则下列说法中正确的是(不计所有粒子重力)( )
如图所示,在x轴上方有垂直于纸面向外的匀强磁场,两带正电且电量相同而质量不同的粒子A和B,已知A、B的质量分别为m1和m2,两粒子以相同的速率从O点以与x轴正方向成α=60°角垂直射入磁场,发现粒子A从a点射出磁场,粒子B从b点射出磁场.若另一与A、B带电量相同而质量不同的粒子C以相同速率与x轴正方向成α=30°角射入x轴上方时,发现它从ab的中点c射出磁场,则下列说法中正确的是(不计所有粒子重力)( )| A. | B粒子在磁场中的运动时间比A粒子在磁场中的运动时间长 | |
| B. | 粒子A、B在磁场中的运动时间相同 | |
| C. | 可以求出C粒子的质量 | |
| D. | C粒子在磁场中作圆周运动的半径一定比B粒子作圆周运动的半径小 |
18.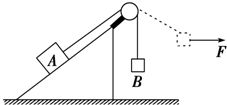 如图所示,斜面体放置于粗糙水平地面上,物块A通过跨过定滑轮的轻质细绳与物块B连接,系统处于静止状态,现对B施加一水平力F使B缓慢地运动,使绳子偏离竖直方向一个角度,在此过程中物块A和斜面体始终处于静止状态,则( )
如图所示,斜面体放置于粗糙水平地面上,物块A通过跨过定滑轮的轻质细绳与物块B连接,系统处于静止状态,现对B施加一水平力F使B缓慢地运动,使绳子偏离竖直方向一个角度,在此过程中物块A和斜面体始终处于静止状态,则( )
 如图所示,斜面体放置于粗糙水平地面上,物块A通过跨过定滑轮的轻质细绳与物块B连接,系统处于静止状态,现对B施加一水平力F使B缓慢地运动,使绳子偏离竖直方向一个角度,在此过程中物块A和斜面体始终处于静止状态,则( )
如图所示,斜面体放置于粗糙水平地面上,物块A通过跨过定滑轮的轻质细绳与物块B连接,系统处于静止状态,现对B施加一水平力F使B缓慢地运动,使绳子偏离竖直方向一个角度,在此过程中物块A和斜面体始终处于静止状态,则( )| A. | 斜面体对物块A的摩擦力一直增大 | B. | 地面对斜面体的支持力一直增大 | ||
| C. | 地面对斜面体的摩擦力一直增大 | D. | 地面对斜面体的支持力保持不变 |
2. 如图所示,在光滑绝缘的水平桌面上有四个小球,带电量分虽为-q、Q、-q、Q.四个小球构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )
如图所示,在光滑绝缘的水平桌面上有四个小球,带电量分虽为-q、Q、-q、Q.四个小球构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )
 如图所示,在光滑绝缘的水平桌面上有四个小球,带电量分虽为-q、Q、-q、Q.四个小球构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )
如图所示,在光滑绝缘的水平桌面上有四个小球,带电量分虽为-q、Q、-q、Q.四个小球构成一个菱形,-q、-q的连线与-q、Q的连线之间的夹角为α.若此系统处于平衡状态,则正确的关系式可能是( )| A. | cos3α=$\frac{q}{8Q}$ | B. | cos3α=$\frac{{q}^{2}}{{Q}^{2}}$ | C. | sin3α=$\frac{Q}{8q}$ | D. | sin3α=$\frac{{Q}^{2}}{{q}^{2}}$ |
3.下列说法正确的是( )
| A. | α粒子散射实验说明原子核内部有复杂的结构 | |
| B. | 质量为m的铀238经过2个半衰期的时间,铀238衰变了的质量为$\frac{1}{4}$m | |
| C. | β衰变所释放的电子是原子核内的中子转化成质子和电子所产生的 | |
| D. | 比较α、β、γ三种射线,α射线电离能力最弱、穿透能力最强 |
 如图,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动.现测得转台半径R=0.5m,离水平地面的高度H=0.8m,物块平抛落地过程水平位移的大小s=0.4m.设物块所受的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2.求
如图,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动.现测得转台半径R=0.5m,离水平地面的高度H=0.8m,物块平抛落地过程水平位移的大小s=0.4m.设物块所受的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2.求 如图所示,一个粗细均匀的平底圆管水平旋转,右端用一橡皮塞塞住,气柱长20cm,此时管内、外压强均匀1.0×10Pa,温度均为27℃;当被封闭气体的温度缓慢降至-3℃时,橡皮塞刚好被推动;继续缓慢降温,直到橡皮塞向内推进5cm.已知圆管的横截面积为4.0×10-5m2,橡皮与圆管间的滑动摩擦力等于最大静摩擦力,大气压强保持不变.求:
如图所示,一个粗细均匀的平底圆管水平旋转,右端用一橡皮塞塞住,气柱长20cm,此时管内、外压强均匀1.0×10Pa,温度均为27℃;当被封闭气体的温度缓慢降至-3℃时,橡皮塞刚好被推动;继续缓慢降温,直到橡皮塞向内推进5cm.已知圆管的横截面积为4.0×10-5m2,橡皮与圆管间的滑动摩擦力等于最大静摩擦力,大气压强保持不变.求: