题目内容
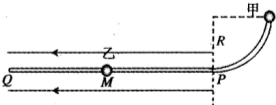 如图所示,两个完全相同、质量都是m的金属小球甲、乙套在光滑绝缘杆上,P左侧杆水平,且处于水平向左场强为E的匀强电场中,右侧是半径为尺的四分之一圆弧杆.甲球带电荷量为q的负电荷,乙球不带电并静止于M处,PM=L.现将甲球从圆弧杆顶端无初速 释放,运动到M时与乙碰撞并粘合在一起向左运动.碰撞时间极短,水平杆足够长.求:
如图所示,两个完全相同、质量都是m的金属小球甲、乙套在光滑绝缘杆上,P左侧杆水平,且处于水平向左场强为E的匀强电场中,右侧是半径为尺的四分之一圆弧杆.甲球带电荷量为q的负电荷,乙球不带电并静止于M处,PM=L.现将甲球从圆弧杆顶端无初速 释放,运动到M时与乙碰撞并粘合在一起向左运动.碰撞时间极短,水平杆足够长.求:(1)甲在碰撞前瞬间的速度大小.
(2)碰撞后甲乙共同向左运动的最大距离.
分析:(1)甲球从下滑到运动到M点的过程中,重力做功mgR,电场力做功-qEL,轨道的支持力不做功,根据动能定理求解甲在碰撞前瞬间的速度大小.
(2)两球碰撞过程,动量守恒,由动量守恒守恒定律求出碰后的共同速度.碰后两球一起向左做匀减速运动,当速度减为零时,向左运动的距离最大,由动能定理求解最大距离.
(2)两球碰撞过程,动量守恒,由动量守恒守恒定律求出碰后的共同速度.碰后两球一起向左做匀减速运动,当速度减为零时,向左运动的距离最大,由动能定理求解最大距离.
解答:解:(1)甲球在运动到M点的过程中,根据动能定理得
mgR-qEL=
mv2-0
解得 v=
(2)设甲、乙碰撞后共同速度为v′,由动量守恒定律得
mv=2mv′
由动能定理得-qEx=0-
×2m?v′2
联立解得:x=
-
答:
(1)甲在碰撞前瞬间的速度大小为
.
(2)碰撞后甲乙共同向左运动的最大距离为
-
.
mgR-qEL=
| 1 |
| 2 |
解得 v=
2gR-
|
(2)设甲、乙碰撞后共同速度为v′,由动量守恒定律得
mv=2mv′
由动能定理得-qEx=0-
| 1 |
| 2 |
联立解得:x=
| mgR |
| 2qE |
| L |
| 2 |
答:
(1)甲在碰撞前瞬间的速度大小为
2gR-
|
(2)碰撞后甲乙共同向左运动的最大距离为
| mgR |
| 2qE |
| L |
| 2 |
点评:本题是含有非弹性碰撞的过程,分析物理过程,把握每个过程的物理规律是关键,碰撞的基本规律是动量守恒.

练习册系列答案
相关题目
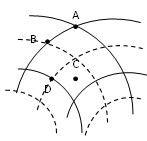
 (2012?金山区一模)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )
(2012?金山区一模)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( ) (2008?上海模拟)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )
(2008?上海模拟)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )