题目内容
13.从离地高x处自由下落的物体,落到地面所用的时间t=$\sqrt{\frac{2x}{g}}$,落地时的速度v=$\sqrt{2gx}$,物体下落$\frac{x}{3}$时和下落全程时的速度之比是$\sqrt{\frac{4}{3}}$,经历的时间之比是$\sqrt{\frac{1}{3}}$.分析 根据自由落体运动的位移时间公式求的下落时间,根据速度时间公式起的落地时的速度,利用平均速度求的全程的速度即可
解答 解:由h=$\frac{1}{2}g{t}^{2}$得:t=$\sqrt{\frac{2x}{g}}$,
落地时的速度为:v=gt=$\sqrt{2gx}$
下落$\frac{x}{3}$的速度为v,则$2g•\frac{x}{3}=v{′}^{2}$,
解得:$v′=\sqrt{\frac{2gx}{3}}$
下落全程的平均速度为:$\overline{v}=\frac{x}{t}=\sqrt{\frac{gx}{2}}$
故$\frac{v′}{\overline{v}}=\sqrt{\frac{4}{3}}$
下落$\frac{x}{3}$所需时间为:t$′=\frac{v′}{g}=\sqrt{\frac{2x}{3g}}$
故$\frac{t′}{t}=\sqrt{\frac{1}{3}}$
故答案为:$\sqrt{\frac{2x}{g}}$,$\sqrt{2gx}$,$\sqrt{\frac{4}{3}}$,$\sqrt{\frac{1}{3}}$
点评 本题主要考查了自由落体运动,关键是灵活运用位移时间公式和速度时间公式即可

练习册系列答案
相关题目
1.质点做直线运动的位移x与时间t的关系为x=5t+t2(各物理量均采用国际单位),则该质点( )
| A. | 任意1s内的速度增量都是1m/s | B. | 任意相邻的1s 内位移差都是2m | ||
| C. | 前2s内的平均速度是6m/s | D. | 第1s内的位移是5m |
8.将一根导线均匀拉制成横截面积为原来$\frac{1}{2}$的细导线,拉制后的细导线电阻是原导线电阻的( )
| A. | 2倍 | B. | 4倍 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
18. 让一质量为m=1kg的小球从某一高度水平抛出,从小球水平抛出到落地过程中,小球速度方向与水平方向间夹角θ的正切值tanθ随时间t变化的关系图象如图所示.重力加速度g=10m/s2,则( )
让一质量为m=1kg的小球从某一高度水平抛出,从小球水平抛出到落地过程中,小球速度方向与水平方向间夹角θ的正切值tanθ随时间t变化的关系图象如图所示.重力加速度g=10m/s2,则( )
 让一质量为m=1kg的小球从某一高度水平抛出,从小球水平抛出到落地过程中,小球速度方向与水平方向间夹角θ的正切值tanθ随时间t变化的关系图象如图所示.重力加速度g=10m/s2,则( )
让一质量为m=1kg的小球从某一高度水平抛出,从小球水平抛出到落地过程中,小球速度方向与水平方向间夹角θ的正切值tanθ随时间t变化的关系图象如图所示.重力加速度g=10m/s2,则( )| A. | 小球水平抛出的初速度为2m/s | B. | 小球抛出点的高度为20m | ||
| C. | 小球落地时的速度大小为20m/s | D. | 小球落地时的动能为425J |
5. 如图所示,竖直放置的光滑圆轨道半径为R,A、B为圆轨道内表面的最低点和最高点,在A、B两位置装有压力传感器,可以测量小球经过该位置时对轨道的压力F.一质量为m的小球置于轨道最低点A处,现给小球一水平向右的初速度v,使其沿圆轨道运动;改变小球的初速度v的大小,测量小球在A、B位置对轨道压力FA、FB的大小,根据测量数据描绘出相应的F-v2图象为相互平行的直线,如图所示.重力加速度为g,则( )
如图所示,竖直放置的光滑圆轨道半径为R,A、B为圆轨道内表面的最低点和最高点,在A、B两位置装有压力传感器,可以测量小球经过该位置时对轨道的压力F.一质量为m的小球置于轨道最低点A处,现给小球一水平向右的初速度v,使其沿圆轨道运动;改变小球的初速度v的大小,测量小球在A、B位置对轨道压力FA、FB的大小,根据测量数据描绘出相应的F-v2图象为相互平行的直线,如图所示.重力加速度为g,则( )
 如图所示,竖直放置的光滑圆轨道半径为R,A、B为圆轨道内表面的最低点和最高点,在A、B两位置装有压力传感器,可以测量小球经过该位置时对轨道的压力F.一质量为m的小球置于轨道最低点A处,现给小球一水平向右的初速度v,使其沿圆轨道运动;改变小球的初速度v的大小,测量小球在A、B位置对轨道压力FA、FB的大小,根据测量数据描绘出相应的F-v2图象为相互平行的直线,如图所示.重力加速度为g,则( )
如图所示,竖直放置的光滑圆轨道半径为R,A、B为圆轨道内表面的最低点和最高点,在A、B两位置装有压力传感器,可以测量小球经过该位置时对轨道的压力F.一质量为m的小球置于轨道最低点A处,现给小球一水平向右的初速度v,使其沿圆轨道运动;改变小球的初速度v的大小,测量小球在A、B位置对轨道压力FA、FB的大小,根据测量数据描绘出相应的F-v2图象为相互平行的直线,如图所示.重力加速度为g,则( )| A. | 图象中的FA-v2图线与FB-v2图线的斜率均为$\frac{R}{m}$ | |
| B. | 图象中F0的数值为6mg | |
| C. | 图象中v0=$\sqrt{5gR}$ | |
| D. | 仅由F-v2图象特点不能判断小球沿圆轨道运动过程机械能是否守恒 |
11.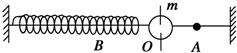 对于弹簧振子,完成如下表格,用斜向上箭头表示增大,用斜向下箭头表示减小.(max 表示最大、min 表示最小)
对于弹簧振子,完成如下表格,用斜向上箭头表示增大,用斜向下箭头表示减小.(max 表示最大、min 表示最小)
 对于弹簧振子,完成如下表格,用斜向上箭头表示增大,用斜向下箭头表示减小.(max 表示最大、min 表示最小)
对于弹簧振子,完成如下表格,用斜向上箭头表示增大,用斜向下箭头表示减小.(max 表示最大、min 表示最小)| A | A→O | O | O→B | B | |
| 位移x | |||||
| 回复力F | |||||
| 加速度a | |||||
| 弹性势能 | |||||
| 速度v | |||||
| 动能 |
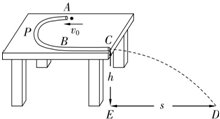 某游乐设施如图所示,由半圆形APB和直线BC组成的细圆管轨道固定在水平桌面上(圆半径比细管内径大得多),轨道内壁光滑.已知APB部分的半径R=0.8m,BC段长L=1.6m.弹射装置将一质量m=0.2kg的小球(可视为质点)以水平初速度v0从A点弹入轨道,小球从C点离开轨道水平抛出,落地点D离C点的水平距离为s=1.6m,桌子的高度h=0.8m,不计空气阻力,取g=10m/s2.求:
某游乐设施如图所示,由半圆形APB和直线BC组成的细圆管轨道固定在水平桌面上(圆半径比细管内径大得多),轨道内壁光滑.已知APB部分的半径R=0.8m,BC段长L=1.6m.弹射装置将一质量m=0.2kg的小球(可视为质点)以水平初速度v0从A点弹入轨道,小球从C点离开轨道水平抛出,落地点D离C点的水平距离为s=1.6m,桌子的高度h=0.8m,不计空气阻力,取g=10m/s2.求: 电梯上升运动的v-t图象如图所示,从图象可知电梯上升前2s的加速度a=3m/s2,前6s位移S=39m,前6S的平均速度V=6.5m/s.
电梯上升运动的v-t图象如图所示,从图象可知电梯上升前2s的加速度a=3m/s2,前6s位移S=39m,前6S的平均速度V=6.5m/s. 有两个相同的全长电阻为9Ω的均匀光滑圆环,固定于一个绝缘的水平台面上,两环分别在两个互相平行的、相距为20cm的竖直面内,两环的连心线恰好与环面垂直,两环面间有方向竖直向下的磁感应强度B=0.865T的匀强磁场,两环的最高点A和C间接有一内阻为0.5Ω的电源,连接导线的电阻不计.今有一根质量为10g,电阻为1.5Ω的棒置于两环内侧且可顺环滑动,而棒恰好静止于如图所示的水平位置,它与圆弧的两接触点P、Q和圆弧最低点间所夹的弧对应的圆心角均为θ=60°,取重力加速度g=10m/s2.试求此电源电动势E的大小.(取$\sqrt{3}$=1.73)
有两个相同的全长电阻为9Ω的均匀光滑圆环,固定于一个绝缘的水平台面上,两环分别在两个互相平行的、相距为20cm的竖直面内,两环的连心线恰好与环面垂直,两环面间有方向竖直向下的磁感应强度B=0.865T的匀强磁场,两环的最高点A和C间接有一内阻为0.5Ω的电源,连接导线的电阻不计.今有一根质量为10g,电阻为1.5Ω的棒置于两环内侧且可顺环滑动,而棒恰好静止于如图所示的水平位置,它与圆弧的两接触点P、Q和圆弧最低点间所夹的弧对应的圆心角均为θ=60°,取重力加速度g=10m/s2.试求此电源电动势E的大小.(取$\sqrt{3}$=1.73)