题目内容
【题目】如图所示,长L=1.5 m、质量M=3 kg的木板静止放在水平面上,质量m=1 kg 的小物块(可视为质点)放在木板的右端,木板和物块间的动摩擦因数μ1=0.1,木板与地面间的动摩擦因数μ2=0.2.现对木板施加一水平向右的恒定拉力F,取g=10 m/s2.

(1)求使物块不掉下去的最大拉力F0(物块受到的最大静摩擦力等于滑动摩擦力).
(2)如果拉力F=21 N恒定不变,经多长时间物块从板上滑下
【答案】(1)12N(2)1s
【解析】(1)物块刚好不掉下去,则物块与木板达到最大静摩擦力,且具有相同的最大加速度a1.对物块有牛顿第二定律得: ![]()
对整体:F0-μ2(M+m)g=(M+m)a1
解得:F0=μ2(M+m)g+(M+m)a1=0.2×(3+1)×10+(3+1)×1N=12N
(2)当拉力F=21N>F0时,物块相对木板滑动.
由牛顿第二定律,F-μ1mg-μ2(M+m)g=Ma2
得:木板的加速度: ![]()
设小物块滑离时经历的时间为t,则: ![]() a2t2-
a2t2-![]() a1t2=L
a1t2=L
解得: 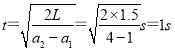 .
.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目