��Ŀ����
����Ŀ����ͼ����ʾ��ˮƽ���ʹ��ij���L=6m�����ʹ�Ƥ���ֵİ뾶��ΪR=0��25m������һС����������Ϊ�ʵ�����һ����ˮƽ�ٶ�v0���ϴ��ʹ�����Ƥ����˳ʱ������ת���������ٶ�Ϊ��ʱ�������뿪���ʹ�B�˺��ڿ����˶���ˮƽ����Ϊs����Ƥ�����Բ�ͬ�Ľ��ٶ��ظ��������������ֻ��ϴ��ʹ��ij���v0���������ɵõ�һЩ��Ӧ�Ħغ�sֵ������Щ��Ӧֵ���������ϲ������������õ���ͼ����ʵ����ʾ�� s- ��ͼ��,����ͼ�б����������gȡ10m/s2 ������
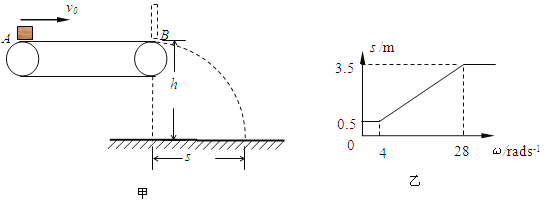
��1��B�˾����ĸ߶�h
��2�����ϴ��ʹ�ʱ�ij���v0�Լ������Ƥ����Ķ�Ħ��������
��3������B�˼�һ��ֱ����P��Ƥ�����Խ��ٶȦء�=16rad/s˳ʱ������ת���������뵲������������ײ��ʱ����t��Ϊ����? �����廬��A��ʱ�ٶ���Ϊv0���ں͵�����ײ����е����ʧ��
���𰸡���1��1��25m��2��5m/s��0��2��3��4s
��������
�����������1����ͼ�ҿ�֪����Ƥ�����Խ��ٶȦ�1=4rad/sʱ�� �����뿪Ƥ����ƽ���˶��ij��ٶ�Ϊ
v1=��1 R =1m/s
ˮƽ����Ϊs=0��5m���� t=s/v=0��5s
h=![]() =1��25m
=1��25m
��2����ͼ���֪�����ءܦ�1=4rad/sʱ,�����ڴ��ʹ���һֱ���٣�
��ţ�ٵڶ����ɵã����ٶȴ�СΪa=��g
����B��ʱ���ٶ�Ϊv1�� �� v02 - v12 =2��gL
���ء�28rad/sʱ�������ڴ��ʹ���һֱ���٣�
����B��ʱ���ٶ�Ϊv2 = ��2 R = 7m/s ��
�� v22 �C v02 =2��gL
��������ʽ��æ�=0��2
v0= 5m/s
��3�������� =16rad/sʱ ��Ƥ���ٶ� v�� = ���� R =4m/s
������v0=5m/s���ٶȿ�ʼ���٣���s��=![]() = 2��25m < L
= 2��25m < L
��������������ǰ�Ѿ����ٵ�v�� = 4m/s
������֪����Ͱ���ײǰ����ٶȴ�С����v�� = 4m/s
 ���˶��ĶԳ��Ե� t' =2 v' /a = 4s
���˶��ĶԳ��Ե� t' =2 v' /a = 4s