题目内容
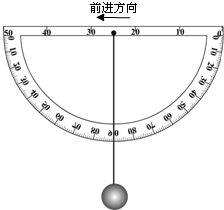
 为了解汽车等交通工具在水平路面上加速或减速过程中的加速度,某同学自行设计了一个测量加速度的工具.原理如下:将量角器固定在汽车上,其平面保持竖直,且直边保持水平并与汽车前进方向平行;再将一个小球系在细绳的一端,细绳的另一端系在量角器的直边中点上,如图所示.当汽车静止时,小球下垂,细绳正好通过90°角的位置,即为加速度零刻度线;当汽车匀加速或匀减速运动时,细绳会沿量角器的平面向后或向前摆动,稳定后可以通过细绳偏离加速度零刻线的角度大小计算出相对应的加速度的值;最后在量角器的不同角度处标出不同的加速度值.(用g表示重力加速度,sin37°=0.6,cos37°=0.8).
为了解汽车等交通工具在水平路面上加速或减速过程中的加速度,某同学自行设计了一个测量加速度的工具.原理如下:将量角器固定在汽车上,其平面保持竖直,且直边保持水平并与汽车前进方向平行;再将一个小球系在细绳的一端,细绳的另一端系在量角器的直边中点上,如图所示.当汽车静止时,小球下垂,细绳正好通过90°角的位置,即为加速度零刻度线;当汽车匀加速或匀减速运动时,细绳会沿量角器的平面向后或向前摆动,稳定后可以通过细绳偏离加速度零刻线的角度大小计算出相对应的加速度的值;最后在量角器的不同角度处标出不同的加速度值.(用g表示重力加速度,sin37°=0.6,cos37°=0.8).(1)通过计算,说明汽车匀加速运动的加速度为0.75g时的刻度应标在量角器上角度为多少度的位置;
(2)设小球的质量为m,求当细绳偏至第(1)问所标的位置时,细绳对小球的拉力大小.
分析:(1)对小球受力分析,受两个力,重力和拉力,小球随汽车向前匀加速运动,加速度向前,合力向前,根据平行四边形定则作图求出合力,再根据牛顿第二定律列式求解;
(2)根据第①小问的图分析即可求出拉力F.
(2)根据第①小问的图分析即可求出拉力F.
解答:解:(1)当汽车以加速度a行驶时,
对小球进行受力分析如图所示
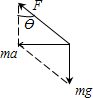
设细绳与竖直方向的夹角为θ,两个力进行合成后有:
mgtanθ=ma
汽车运行的加速度a=gtanθ
当a=0.75g时,tanθ=0.75,θ=37°
故0.75g应标在量角器的53°位置)
(2)由受力分析图可知
拉力 F=
解得 F=
mg
即当细绳偏至第(1)问所标的位置时,细绳对小球的拉力大小为
mg.
对小球进行受力分析如图所示

设细绳与竖直方向的夹角为θ,两个力进行合成后有:
mgtanθ=ma
汽车运行的加速度a=gtanθ
当a=0.75g时,tanθ=0.75,θ=37°
故0.75g应标在量角器的53°位置)
(2)由受力分析图可知
拉力 F=
| (mg)2+(ma)2 |
解得 F=
| 5 |
| 4 |
即当细绳偏至第(1)问所标的位置时,细绳对小球的拉力大小为
| 5 |
| 4 |
点评:本题关键分析出小球的运动情况和受力情况,根据平行四边形定则作图求出合力,再根据牛顿第二定律列式求解出加速度的一般表达式分析.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
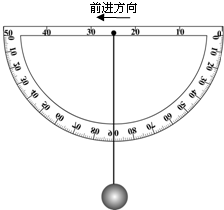 为了解汽车等交通工具在水平路面上加速或减速过程中的加速度,某同学自行设计了一个测量加速度的工具.原理如下:将量角器固定在汽车上,其平面保持竖直,且直边保持水平并与汽车前进方向平行;再将一个小球系在细绳的一端,细绳的另一端系在量角器的直边中点上,如图所示.当汽车静止时,小球下垂,细绳正好通过90°角的位置,即为加速度零刻度线;当汽车匀加速或匀减速运动时,细绳会沿量角器的平面向后或向前摆动,稳定后可以通过细绳偏离加速度零刻线的角度大小计算出相对应的加速度的值;最后在量角器的不同角度处标出不同的加速度值.(用g表示重力加速度,sin37°=0.6,cos37°=0.8).
为了解汽车等交通工具在水平路面上加速或减速过程中的加速度,某同学自行设计了一个测量加速度的工具.原理如下:将量角器固定在汽车上,其平面保持竖直,且直边保持水平并与汽车前进方向平行;再将一个小球系在细绳的一端,细绳的另一端系在量角器的直边中点上,如图所示.当汽车静止时,小球下垂,细绳正好通过90°角的位置,即为加速度零刻度线;当汽车匀加速或匀减速运动时,细绳会沿量角器的平面向后或向前摆动,稳定后可以通过细绳偏离加速度零刻线的角度大小计算出相对应的加速度的值;最后在量角器的不同角度处标出不同的加速度值.(用g表示重力加速度,sin37°=0.6,cos37°=0.8).