题目内容
如图所示,A是置于光滑水平面上的表面绝缘、质量m1=1kg的小车,小车的左端放置有一个可视为质点的、质量m2=2kg、电荷量q=+1×10-4 C的小物块B,距小车右端s=2m处有一竖直的墙壁.小车所在空间有一个可以通过开关控制其有、无的水平向右的匀强电场,电场强度的大小为E=3×104N/C.若小车A和小物块B一起由静止开始运动,且在小车与墙壁碰撞的瞬间撤去电场;碰撞时间忽略不计,碰撞过程无机械能的损失;小物块B始终未到达小车A的右端,它们之问的动摩擦因数μ=0.2,最大静摩擦力等于滑动摩擦力.小车不带电,g取10m/s2.求:
(1)有电场作用时小车A所受的摩擦力大小和方向?
(2)小车A第一次与墙壁相碰后向左运动的最远距离为多少?
(3)小车A第二次与墙壁相碰时的速度为多少?
(4)要使小物块B最终不滑离小车A,小车的长度至少多长?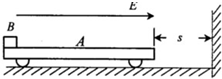
(1)有电场作用时小车A所受的摩擦力大小和方向?
(2)小车A第一次与墙壁相碰后向左运动的最远距离为多少?
(3)小车A第二次与墙壁相碰时的速度为多少?
(4)要使小物块B最终不滑离小车A,小车的长度至少多长?

(1)假设小车A与小物块B相对静止,以A、B整体为研究对象
由牛顿第二定律得qE=(m1+m2)a
解得a=1 m/s2
再以小车A为研究对象,设它受到的静摩擦力为FBA,A、B之间的最大静摩擦力为Fmax,
由牛顿第二定律得FBA=m1a=1N,Fmax=μm2g=4N
因FBA<Fmax,故假设成立.小车A所受的摩擦力大小为1N,方向水平向右
(2)设小车A和小物块B第一次与墙壁相碰前瞬间的速度为v0.
由运动学规律有v02=2as
解得v0=2m/s
小车A与墙壁相碰后瞬间速度大小不变,方向向左,小物块B速度不变.由于B的动量大于A的动量,因此A向左做匀减速运动的速度减为零时,向左运动的距离最远,设这个距离为s1
由动能定理有μm2gs1=
m1v02
解得s1=0.5m
(3)接着小车A又向右做初速度为零的匀加速运动,假设小车A和小物块B先达到共同速度后再与墙壁相碰,且设第二次与墙壁相碰前瞬间的速度为v共.
由动量守恒定律得m2v0-m1v0=(m1+m2)v共
解得v共=
m/s
设小车A由速度为零到达到共同速度所通过的距离为s2
由动能定理有μm2gs2=
m1
解得s2=
m<s1,所以,假设成立
(4)小车A与小物块B最终将停止在墙角处,设小车至少长L
由能量守恒定律得μm2gL=
(m1+m2)
代入数据得L=1.5 m
答:(1)有电场作用时小车A所受的摩擦力大小为1N,方向水平向右;(2)小车A第一次与墙壁相碰后向左运动的最远距离为0.5m;(3)小车A第二次与墙壁相碰时的速度为
m/s;(4)要使小物块B最终不滑离小车A,小车的长度至少为1.5 m.
由牛顿第二定律得qE=(m1+m2)a
解得a=1 m/s2
再以小车A为研究对象,设它受到的静摩擦力为FBA,A、B之间的最大静摩擦力为Fmax,
由牛顿第二定律得FBA=m1a=1N,Fmax=μm2g=4N
因FBA<Fmax,故假设成立.小车A所受的摩擦力大小为1N,方向水平向右
(2)设小车A和小物块B第一次与墙壁相碰前瞬间的速度为v0.
由运动学规律有v02=2as
解得v0=2m/s
小车A与墙壁相碰后瞬间速度大小不变,方向向左,小物块B速度不变.由于B的动量大于A的动量,因此A向左做匀减速运动的速度减为零时,向左运动的距离最远,设这个距离为s1
由动能定理有μm2gs1=
| 1 |
| 2 |
解得s1=0.5m
(3)接着小车A又向右做初速度为零的匀加速运动,假设小车A和小物块B先达到共同速度后再与墙壁相碰,且设第二次与墙壁相碰前瞬间的速度为v共.
由动量守恒定律得m2v0-m1v0=(m1+m2)v共
解得v共=
| 2 |
| 3 |
设小车A由速度为零到达到共同速度所通过的距离为s2
由动能定理有μm2gs2=
| 1 |
| 2 |
| v | 2共 |
解得s2=
| 1 |
| 18 |
(4)小车A与小物块B最终将停止在墙角处,设小车至少长L
由能量守恒定律得μm2gL=
| 1 |
| 2 |
| v | 20 |
代入数据得L=1.5 m
答:(1)有电场作用时小车A所受的摩擦力大小为1N,方向水平向右;(2)小车A第一次与墙壁相碰后向左运动的最远距离为0.5m;(3)小车A第二次与墙壁相碰时的速度为
| 2 |
| 3 |

练习册系列答案
相关题目
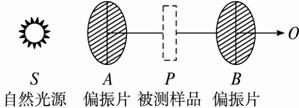
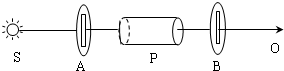 (2010?云南模拟)利用旋光仪这种仪器可以用来测量糖溶液的浓度,从而测定含糖量.其原理是:偏振光通过糖的水溶液后,若迎着射来的光线看,偏振方向会以传播方向为轴线,旋转一个角度θ,这一角度称为“旋光角”,θ的值与糖溶液的浓度有关.将θ的测量值与标准值相比较,就能确定被测样品的含糖量了.如图所示,S是自然光源,A、B是偏振片,转动B,使到达O处的光最强,然后将被测样品P置于A、B之间,则下列说法中正确的是( )
(2010?云南模拟)利用旋光仪这种仪器可以用来测量糖溶液的浓度,从而测定含糖量.其原理是:偏振光通过糖的水溶液后,若迎着射来的光线看,偏振方向会以传播方向为轴线,旋转一个角度θ,这一角度称为“旋光角”,θ的值与糖溶液的浓度有关.将θ的测量值与标准值相比较,就能确定被测样品的含糖量了.如图所示,S是自然光源,A、B是偏振片,转动B,使到达O处的光最强,然后将被测样品P置于A、B之间,则下列说法中正确的是( ) 利用旋光仪这种仪器可以用来测量糖溶液的浓度,从而测定含糖量.其原理是:偏振光通过糖的水溶液后,若迎着射来的光线看,偏振方向会以传播方向为轴线,旋转一个角度θ,这一角度称为“旋光角”,θ的值与糖溶液的浓度有关.将θ的测量值与标准值相比较,就能确定被测样品的含糖量了.如图所示,S是自然光源,A、B是偏振片,转动B,使到达O处的光最强,然后将被测样品P置于A、B之间,则下列说法中错误的是( )
利用旋光仪这种仪器可以用来测量糖溶液的浓度,从而测定含糖量.其原理是:偏振光通过糖的水溶液后,若迎着射来的光线看,偏振方向会以传播方向为轴线,旋转一个角度θ,这一角度称为“旋光角”,θ的值与糖溶液的浓度有关.将θ的测量值与标准值相比较,就能确定被测样品的含糖量了.如图所示,S是自然光源,A、B是偏振片,转动B,使到达O处的光最强,然后将被测样品P置于A、B之间,则下列说法中错误的是( )