题目内容
【题目】如图所示,A、B、C三个小物块放置在光滑水平面上,A靠在墙壁,A、B之间用轻弹簧连接,它们的质量分别为mA=m,mB=2m,mC=m.现给C一水平向左的初速度v0,C与B发生碰撞并粘在一起.试求:
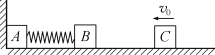
(1)A离开墙前,弹簧的最大弹性势能;
(2)A离开墙后,C的最小速度.
【答案】(1)![]() mv02 (2)
mv02 (2)![]()
【解析】
试题分析: (1)设C与B发生碰撞粘在一起时的速度为v,由动量守恒定律得mCv0=(mC+mB)v,解得v=![]()
设A离开墙前,弹簧的最大弹性势能为Epm,由能量守恒定律得Epm=![]() (mC+mB)v2,联立解得 Epm=
(mC+mB)v2,联立解得 Epm=![]() mv
mv
(2)弹簧恢复原长状态,C、B的速度大小为v,方向水平向右.当弹簧下一次处于原长状态时,B、C的速度最小且为vC,此时A的速度为vA.
由动量守恒定律得(mC+mB)v=mAvA+(mC+mB)vC
由能量守恒定律得
![]() (mC+mB)v2=
(mC+mB)v2=![]() mAvA2+
mAvA2+![]() (mC+mB)vC2
(mC+mB)vC2
联立解得 vC=![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目