题目内容
平直公路上有甲、乙两辆汽车,甲以0.5 m/s2的加速度由静止开始行驶,乙在甲的前方200 m处以5 m/s的速度做同方向的匀速运动.问:
(1)甲何时追上乙?甲追上乙时甲的速度为多大?此时甲离出发点多远?
(2)在追赶过程中,甲、乙之间何时有最大距离?这个距离为多大?
(1)甲何时追上乙?甲追上乙时甲的速度为多大?此时甲离出发点多远?
(2)在追赶过程中,甲、乙之间何时有最大距离?这个距离为多大?
(1)4 s后 20 m/s 400 m (2)甲行驶10 s时,甲、乙间的距离最大,最大距离为225 m
本题考查匀变速直线运动的追击相遇问题,当甲追上乙的时候两者位移相同,根据这个等量关系列式可求解运动时间,当两者速度相同的时候两者距离有最大值,根据速度相同求得距离最大的时刻,再由各自的运动位移与时间的关系求得两者的位移大小,取差值即可
甲追上乙时,x甲=x0+x乙,t甲=t乙
(1)设甲经时间t追上乙,则有x甲=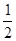 a甲t2,x乙=v乙t.根据追及条件,有
a甲t2,x乙=v乙t.根据追及条件,有
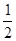 a甲t2=v乙t,代入数值,解得t="40" s或t="-20" s(舍去).
a甲t2=v乙t,代入数值,解得t="40" s或t="-20" s(舍去).
这时甲的速度v甲=a甲t="0.5×40" m/s="20" m/s,甲离出发点的位移x甲=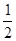 a甲t2=
a甲t2=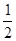 ×0.5×402 m="400" m.
×0.5×402 m="400" m.
(2)在追赶过程中,当甲的速度小于乙的速度时,甲、乙之间的距离仍在增大,但当甲的速度大于乙的速度时,甲、乙之间的距离便减小.当二者速度相等时,甲、乙之间的距离达到最大值.由a甲t=v乙,得t="10" s,即甲在10 s末离乙的距离最大.
xmax=x0+v乙t-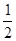 a甲t2=(200+5×10-
a甲t2=(200+5×10-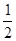 ×0.5×102) m="225" m.
×0.5×102) m="225" m.
甲追上乙时,x甲=x0+x乙,t甲=t乙
(1)设甲经时间t追上乙,则有x甲=
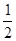 a甲t2,x乙=v乙t.根据追及条件,有
a甲t2,x乙=v乙t.根据追及条件,有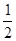 a甲t2=v乙t,代入数值,解得t="40" s或t="-20" s(舍去).
a甲t2=v乙t,代入数值,解得t="40" s或t="-20" s(舍去).这时甲的速度v甲=a甲t="0.5×40" m/s="20" m/s,甲离出发点的位移x甲=
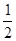 a甲t2=
a甲t2=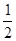 ×0.5×402 m="400" m.
×0.5×402 m="400" m.(2)在追赶过程中,当甲的速度小于乙的速度时,甲、乙之间的距离仍在增大,但当甲的速度大于乙的速度时,甲、乙之间的距离便减小.当二者速度相等时,甲、乙之间的距离达到最大值.由a甲t=v乙,得t="10" s,即甲在10 s末离乙的距离最大.
xmax=x0+v乙t-
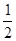 a甲t2=(200+5×10-
a甲t2=(200+5×10-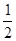 ×0.5×102) m="225" m.
×0.5×102) m="225" m.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
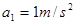 由静止开始作匀加速直线运动,乙车落后
由静止开始作匀加速直线运动,乙车落后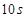 钟在同一地点由静止开始,以加速度
钟在同一地点由静止开始,以加速度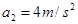 作匀加速直线运动,两车的运动方向相同,求:
作匀加速直线运动,两车的运动方向相同,求: