题目内容
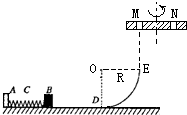 如图所示,水平桌面上有一轻弹簧,左端固定在A点,自然状态时其右端位于B点.B点右侧相距为5R的D处有一竖直固定的光滑四分之一圆弧轨道DE,其半径为R,E点切线竖直,用质量为M的物块将弹簧缓慢压缩到C点,释放后弹簧恢复原长时物块恰停止在B点.用同种材料、质量为m的物块将弹簧缓慢压缩到C点释放,物块到达B点时速度为v0=3
如图所示,水平桌面上有一轻弹簧,左端固定在A点,自然状态时其右端位于B点.B点右侧相距为5R的D处有一竖直固定的光滑四分之一圆弧轨道DE,其半径为R,E点切线竖直,用质量为M的物块将弹簧缓慢压缩到C点,释放后弹簧恢复原长时物块恰停止在B点.用同种材料、质量为m的物块将弹簧缓慢压缩到C点释放,物块到达B点时速度为v0=3| gR |
(1)BC间距离;
(2)m到达D点时对轨道的压力;
(3)平台转动的角速度为ω.
分析:(1)用质量为M和质量为m的两个物块将弹簧缓慢压缩到C点时,弹簧具有的弹性势能相等.用M弹簧压缩弹簧释放后,弹簧的弹性势能转化为内能,用m压缩弹簧释放后,弹性势能转化为物体m的动能、内能.根据功能关系,求解BC间距离.
(2)由B点运动到D点的过程中,由动能定理求出物块在D点时的速度大小,由牛顿运动定律求解m到达D点时对轨道的压力.
(3)物块m从D点到竖直上抛最高点的过程中,机械能守恒,可求出物块m从D点通过小孔M所能达到的距M点的最大高度h,由h=
gt2求出竖直上抛运动的时间2t,物块再次落入小孔N过程中,根据转盘运动的周期性有:T=(n+
)×2t(n=0、1、2、3…),又角速度ω=
联立解得角速度.
(2)由B点运动到D点的过程中,由动能定理求出物块在D点时的速度大小,由牛顿运动定律求解m到达D点时对轨道的压力.
(3)物块m从D点到竖直上抛最高点的过程中,机械能守恒,可求出物块m从D点通过小孔M所能达到的距M点的最大高度h,由h=
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| T |
解答:解:(1)设BC间距离为x,根据能量关系有:
弹性势能Ep=μMgx=μmgx+
m
由于v0=3
解得:x=
;
(2)设物块m到达D点时的速率为v,由B点运动到D点的过程中,由动能定理可得:
-μmg×5R=
mv2-
m
物块在D点时,根据牛顿第二定律:FN-mg=m
解得:FN=9mg
由牛顿第三定律可知,物块对轨道的压力为:FN′=FN=9mg.
(3)设物块m从D点通过小孔M所能达到的距M点的最大高度为h,
由动能定理可得:-mg(h+2R)=0-
mv2
设物块m从最高点落回N孔的时间为t,根据对称性有:h=
gt2
物块再次落入小孔N过程中,对转盘根据周期性有:T=(n+
)×2t(n=0、1、2、3…)
又ω=
联立解得:ω=
.
答:(1)BC间距离是
;
(2)m到达D点时对轨道的压力是9mg;
(3)平台转动的角速度为ω是
(n=0、1、2、3…).
弹性势能Ep=μMgx=μmgx+
| 1 |
| 2 |
| v | 2 0 |
由于v0=3
| gR |
| 15mR |
| M-m |
(2)设物块m到达D点时的速率为v,由B点运动到D点的过程中,由动能定理可得:
-μmg×5R=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
物块在D点时,根据牛顿第二定律:FN-mg=m
| v2 |
| R |
解得:FN=9mg
由牛顿第三定律可知,物块对轨道的压力为:FN′=FN=9mg.
(3)设物块m从D点通过小孔M所能达到的距M点的最大高度为h,
由动能定理可得:-mg(h+2R)=0-
| 1 |
| 2 |
设物块m从最高点落回N孔的时间为t,根据对称性有:h=
| 1 |
| 2 |
物块再次落入小孔N过程中,对转盘根据周期性有:T=(n+
| 1 |
| 2 |
又ω=
| 2π |
| T |
π
| ||
| R(2n+1) |
答:(1)BC间距离是
| 15mR |
| M-m |
(2)m到达D点时对轨道的压力是9mg;
(3)平台转动的角速度为ω是
π
| ||
| R(2n+1) |
点评:本题是复杂的力学综合题,分析物体的运动过程,把握解题规律是关键,难点是抓住转盘运动的周期性,得到转盘的周期与竖直上抛运动时间的关系.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,以地面为零势能面,其机械能的表达式正确的是( )
如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,以地面为零势能面,其机械能的表达式正确的是( )A、
| ||||
B、
| ||||
| C、mgH-mgh | ||||
D、
|
如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,其动能的表达式正确的是( ) 
A. | B. |
| C.mgH-mgh | D. |





 B.
B.


 B.
B.
