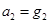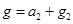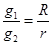题目内容
地球同步卫星到地心距离r可由r3=
,求出已知式中a的单位是m,b的单是s,c的单位是m/s2,则( )
| a2b2c |
| 4π2 |
分析:地球同步卫星公转周期等于地球自转的周期,万有引力等于向心力,轨道平面与赤道平面共面.
解答:解:物体在万有引力作用下做匀速圆周运动,其所需的向心力由万有引力提供,
即:
=
r
整理得到:r3=
此表达式和题目所给的表达式还有不同之处,那么我们可以用黄金代换:GM=gR2(R是地球半径)
代入得到:r3=
结合题目所给单位,a的单位是s,则a对应同步卫星的周期T,也是地球自转周期T,b的单位是m,则b对应地球半径R,
c的单位米每二次方秒,则c对应重力加速度g
所以A正确,B、C、D错误
故选A.
即:
| GMm |
| r2 |
| m4π2 |
| T2 |
整理得到:r3=
| GMT2 |
| 4π2 |
此表达式和题目所给的表达式还有不同之处,那么我们可以用黄金代换:GM=gR2(R是地球半径)
代入得到:r3=
| gR2T2 |
| 4π2 |
结合题目所给单位,a的单位是s,则a对应同步卫星的周期T,也是地球自转周期T,b的单位是m,则b对应地球半径R,
c的单位米每二次方秒,则c对应重力加速度g
所以A正确,B、C、D错误
故选A.
点评:同步卫星的五个“一定”
(1)轨道平面一定(2)周期一定(3)角速度一定(4)高度一定(5)速度一定.通过以上五个方面加深对同步卫星的理解.
(1)轨道平面一定(2)周期一定(3)角速度一定(4)高度一定(5)速度一定.通过以上五个方面加深对同步卫星的理解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
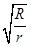
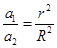 B.
B.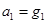 ,
,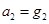 C.
C.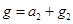 D.
D.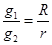
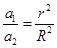
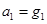 ,
,