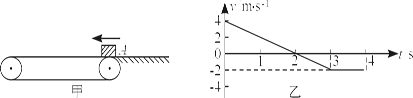题目内容
质量为4.0千克的物体A静止在水平桌面上.另一个质量为2.0千克的物体B以5.0米/秒的水平速度与物体A相撞,碰撞后物体B以1.0米/秒的速度反向弹回.则碰后A的速度为( )
分析:碰撞过程中系统动量守恒,由动量守恒定律可以求出A的速度;
解答:解:AB组成的系统动量守恒,以B的初速度方向为正方向,由动量守恒定律得:
mBvB=mBvB′+mAvA,
即:2×5=2×(-1)+4×vA,
解得:vA=3m/s,速度方向与正方向相同.
故选:A.
mBvB=mBvB′+mAvA,
即:2×5=2×(-1)+4×vA,
解得:vA=3m/s,速度方向与正方向相同.
故选:A.
点评:熟练应用动量守恒定律即可正确解题;应用动量守恒定律解题时,注意正方向的选择.

练习册系列答案
相关题目
如图甲所示,绷紧的水平传送带始终以恒定速率运行,质量m =" 2.0" 千克的小物块从与传送带等高的光滑水平地面上的A处滑上传送带。若从小物块滑上传送带开始计时,小物块在传送带上运动的v—t图象(以地为参考系)如图乙所示,g取10 m/s2,下列判断正确的是( )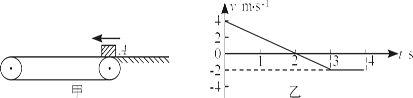
| A.传送带沿逆时针方向运动 |
| B.摩擦力对物块做的功为12焦耳 |
| C.系统共增加了36焦耳的热量 |
| D.物块与传送带间摩擦因数为0.4 |