题目内容
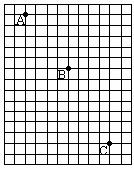
如图所示,有一长为L=0.9m的细线,细线的一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在竖直面内做完整的圆周运动。已知水平地面上的C点位于O点正下方,且到O点的距离为h=1.9m,不计空气阻力。(g取10m/s2)
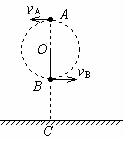
(1)求小球通过最高点A时的速度vA;
(2)若小球通过最低点B时,细线对小球的拉力T恰好为小球重力的6倍,且小球经过B点的瞬间让细线断裂,求小球落地点到C点的距离。

(1)求小球通过最高点A时的速度vA;
(2)若小球通过最低点B时,细线对小球的拉力T恰好为小球重力的6倍,且小球经过B点的瞬间让细线断裂,求小球落地点到C点的距离。
(1)3m/s(2)3m
试题分析:(1)小球恰好能做完整的圆周运动,则小球通过A点时细线的拉力刚好为零
根据向心力公式有:
 2分
2分解得:
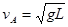 =3m/s 2分
=3m/s 2分(2)小球在B点时根据牛顿第二定律有:
 1分
1分 由已知T=6mg。
解得小球在B点的速度大小为
 1分
1分细线断裂后,小球从B点开始做平抛运动,则由平抛运动的规律得:
竖直方向上h-L=gt2/2 1分
水平方向上 x=vBt 1分
解得:x=3m 1分
即小球落地点到C点的距离为3m。
点评:本题难度较小,刚好通过最高点的最小速度是只由重力提供向心力,在B点之后小球做平抛运动,根据各分运动特点求解

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
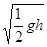
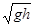
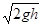
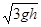

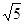 m/s
m/s 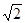 m
m