题目内容
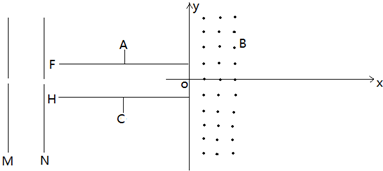
2. 如图所示,一固定斜面与水平面成θ=37°角,其底端O处有一固定粘性挡板,斜面上a、b两点,a、O间的距离为l1=1.5m,a、b间的距离为l2=3.5m.一质量为m1=1kg的物体A静止在a点,另一质量为m2=2kg的物体B从b点以v0=4m/s的速度沿斜面向下运动.A与B、A与挡板相碰时均立即粘在一起且作用时间极短.已知A、B与斜面间的动摩擦因素均为μ=$\frac{7}{8}$,A、B均可看着质点,sin37°=0.6、cos37°=0.8,g=10m/s2.求物体A与挡板相碰时,挡板对物体A的冲量(A、B碰撞后作为一个物体,与挡板碰撞瞬间其重力和斜面对它们的摩擦力忽略不计)
如图所示,一固定斜面与水平面成θ=37°角,其底端O处有一固定粘性挡板,斜面上a、b两点,a、O间的距离为l1=1.5m,a、b间的距离为l2=3.5m.一质量为m1=1kg的物体A静止在a点,另一质量为m2=2kg的物体B从b点以v0=4m/s的速度沿斜面向下运动.A与B、A与挡板相碰时均立即粘在一起且作用时间极短.已知A、B与斜面间的动摩擦因素均为μ=$\frac{7}{8}$,A、B均可看着质点,sin37°=0.6、cos37°=0.8,g=10m/s2.求物体A与挡板相碰时,挡板对物体A的冲量(A、B碰撞后作为一个物体,与挡板碰撞瞬间其重力和斜面对它们的摩擦力忽略不计)
分析 应用动能定理求出B与A碰撞前B的速度,A、B碰撞过程系统动量守恒,应用动量守恒定律可以求出碰撞后的共同速度,然后应用动能定理求出AB与挡板碰撞前的速度,然后应用动量定理可以求出挡板对物体的冲量.
解答 解:设B与A相碰到的速度为v1,B从b运动至a过程中,
由动能定理得:(m2gsinθ-μm2gcosθ)l2=$\frac{1}{2}$m2v12-$\frac{1}{2}$m2v02,
代入数据解得:v1=3m/s,
A与B相碰时系统动量守恒,以平行于斜面向下为正方向,
由动量守恒定律得:m2v1=(m1+m2)v2,代入数据解得:v2=2m/s,
A、B一起向下滑至与档板相碰前,设其速度为v3,由动能定理得:
(m1+m2)g(sinθ-μcosθ)l1═$\frac{1}{2}$(m1+m2)v32-$\frac{1}{2}$(m1+m2)v22,
代入数据解得:v3=1m/s,
以向下为正方向,档板与A相碰,由动量定理得:
I=0-(m1+m2)v3,代入数据解得:I=-3N•m,负号表示方向平行于斜面向上;
答:物体A与挡板相碰时,挡板对物体A的冲量大小为:3N•m,方向:平行于斜面向上.
点评 本题考查了求挡板对物体的冲量,分析清楚物体的运动过程,应用动能定理、动量守恒定律、动量定理即可解题,应用动量守恒定律与动量定理解题时要注意正方向的选择.

练习册系列答案
相关题目
12.关于地球同步卫星,下列说法错误的是( )
| A. | 它一定在赤道上空运行 | |
| B. | 它运行的线速度等于第一宇宙速度 | |
| C. | 各国发射的这种卫星轨道半径都一样 | |
| D. | 它相对地面静止,跟地球自转同步 |
10.下列不是相对论的内容的是( )
| A. | 时间的相对性 | |
| B. | 尺缩效应 | |
| C. | 时钟变慢 | |
| D. | 质量不变,因为它是物体的固有属性,与运动状态无关 |
14.阴极射线管中加高电压的作用是( )
| A. | 使管内的气体电离 | |
| B. | 使阴极发出阴极射线 | |
| C. | 使管内障碍物的电势升高 | |
| D. | 使管内产生前电场,电场力做功使电子加速 |
11.下列说法正确的是( )
| A. | 卢瑟福通过α粒子散射实验建立了原子的核式结构模型 | |
| B. | 宏观物体的物质波波长非常小,极易观察到它的波动性 | |
| C. | β衰变现象说明电子是原子核的组成部分 | |
| D. | 对于任何一种金属都存在一个“最大波长”,入射光的波长必须小于这个波长,才能产生光电效应现象 | |
| E. | 根据玻尔理论可知,氢原子辐射出一个光子后,氢原子的电势能减小,核外电子的运动加速度增大 |


 如图所示,水平轨道与半径R=0.2m的$\frac{1}{4}$圆弧轨道AB平滑连接,B点正上方有一离B点h=0.05m的旋转平台,沿平台直径方向开有两个离轴心距离相等的小孔P、Q.一质量m1=0.3kg的小球a在水平轨道上以v0=5m/s的速度向右运动,与静止在圆弧轨道最低点A,质量m2=0.2kg的小球b相碰并立即粘在一起,后沿圆弧轨道上升.小孔P、Q的孔径大于小球a、b结合体的尺寸,重力加速度g=10m/s2,不计旋转平台的厚度及各处摩擦.求:
如图所示,水平轨道与半径R=0.2m的$\frac{1}{4}$圆弧轨道AB平滑连接,B点正上方有一离B点h=0.05m的旋转平台,沿平台直径方向开有两个离轴心距离相等的小孔P、Q.一质量m1=0.3kg的小球a在水平轨道上以v0=5m/s的速度向右运动,与静止在圆弧轨道最低点A,质量m2=0.2kg的小球b相碰并立即粘在一起,后沿圆弧轨道上升.小孔P、Q的孔径大于小球a、b结合体的尺寸,重力加速度g=10m/s2,不计旋转平台的厚度及各处摩擦.求: