题目内容
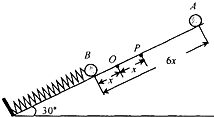 如图所示,倾角30°的光滑固定斜面的底端安有一个挡板,斜面上放有一根轻质弹簧,弹簧的一端固定在挡板上,另一端连接着质量m=0.2kg的小球B,B球平衡时,弹簧的压缩量为x(图中O点是弹簧不连接B球时自由端的位置).今有另一形态大小和B球相同的A球从距B球6x处的斜面上无初速度滑下,它与B球碰撞后粘合在了一起,它们沿斜面向下到达最低点后又沿斜面向上运动,其向上运动到达最高点为P点,P到O的距离也为x.若两小球均可视为质点,且已知同一根弹簧的弹性势能大小仅由弹簧的形变量决定,整个过程中弹簧的形变始终未超过弹性限度,试求:
如图所示,倾角30°的光滑固定斜面的底端安有一个挡板,斜面上放有一根轻质弹簧,弹簧的一端固定在挡板上,另一端连接着质量m=0.2kg的小球B,B球平衡时,弹簧的压缩量为x(图中O点是弹簧不连接B球时自由端的位置).今有另一形态大小和B球相同的A球从距B球6x处的斜面上无初速度滑下,它与B球碰撞后粘合在了一起,它们沿斜面向下到达最低点后又沿斜面向上运动,其向上运动到达最高点为P点,P到O的距离也为x.若两小球均可视为质点,且已知同一根弹簧的弹性势能大小仅由弹簧的形变量决定,整个过程中弹簧的形变始终未超过弹性限度,试求:(1)A球下滑6x即将与B球碰撞时的A球的速度(假设题中x是已知量);
(2)A球的质量(假设题中x是未知量).
分析:(1)A球下滑6x,与B球碰撞前的过程,只有重力做功,A球的机械能守恒,据此定律列式求解即可.
(2)A与B球碰撞过程中,遵守动量守恒,可列式动量守恒方程;碰后,A、B和弹簧组成的系统在运动过程中,机械能守恒,再由机械能守恒定律列出方程,结合第1问的结果,即可求解A球的质量.
(2)A与B球碰撞过程中,遵守动量守恒,可列式动量守恒方程;碰后,A、B和弹簧组成的系统在运动过程中,机械能守恒,再由机械能守恒定律列出方程,结合第1问的结果,即可求解A球的质量.
解答:解:(1)设A球的质量为M,A与B球碰撞前后,A球的速度分别是v1和v2,因A球滑下过程中,机械能守恒,有:
Mg(6x)sin30°=
M
解得:v1=
①
(2)又因A与B球碰撞过程中,动量守恒,有 Mv1=(m+M)
②
碰后,A、B和弹簧组成的系统在运动过程中,机械能守恒.因碰撞时弹簧的压缩量与A、B到达P点时弹簧的伸长量相等,
则有:(m+M)g(2x)sin30°=
(m+M)
解得:v2=
③
将①、③代入②式解得:M=
④
代入数据,解得:M=
kg
答:
(1)A球下滑6x即将与B球碰撞时的A球的速度为
.
(2)A球的质量为
kg.
Mg(6x)sin30°=
| 1 |
| 2 |
| v | 2 1 |
解得:v1=
| 6xg |
(2)又因A与B球碰撞过程中,动量守恒,有 Mv1=(m+M)
| v | 2 |
碰后,A、B和弹簧组成的系统在运动过程中,机械能守恒.因碰撞时弹簧的压缩量与A、B到达P点时弹簧的伸长量相等,
则有:(m+M)g(2x)sin30°=
| 1 |
| 2 |
| v | 2 2 |
解得:v2=
| 2xg |
将①、③代入②式解得:M=
(1+
| ||
| 2 |
代入数据,解得:M=
1+
| ||
| 10 |
答:
(1)A球下滑6x即将与B球碰撞时的A球的速度为
| 6xg |
(2)A球的质量为
1+
| ||
| 10 |
点评:分析清楚物体运动过程、抓住碰撞时弹簧的压缩量与A、B到达P点时弹簧的伸长量相等,弹簧势能相等是关键,应用机械能守恒定律、动量守恒定律即可正确解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?双流县模拟)如图所示,倾角θ=30°、宽度L=1m的足够长的U形平行光滑金属导轨固定在磁感应强度B=1T,范围足够大的匀强磁场中,磁场方向垂直于斜面向下.用平行于轨道的牵引力拉一根质量m=0.2kg、电阻R=1Ω放在导轨上的金属棒ab,使之由静止沿轨道向上运动,牵引力做功的功率恒为6W,当金属棒移动2.8m时,获得稳定速度,在此过程中金属棒产生的热量为5.8J,不计导轨电阻及一切摩擦,取g=10m/s2.求:
(2011?双流县模拟)如图所示,倾角θ=30°、宽度L=1m的足够长的U形平行光滑金属导轨固定在磁感应强度B=1T,范围足够大的匀强磁场中,磁场方向垂直于斜面向下.用平行于轨道的牵引力拉一根质量m=0.2kg、电阻R=1Ω放在导轨上的金属棒ab,使之由静止沿轨道向上运动,牵引力做功的功率恒为6W,当金属棒移动2.8m时,获得稳定速度,在此过程中金属棒产生的热量为5.8J,不计导轨电阻及一切摩擦,取g=10m/s2.求: 如图所示,倾角θ=30°、长L=2.7m的斜面,底端与一个光滑的1/4圆弧平滑连接,圆弧底端切线水平.一个质量为m=1kg的质点从斜面最高点A沿斜面下滑,经过斜面底端B恰好到达圆弧最高点C,又从圆弧滑回,能上升到斜面上的D点,再由D点由斜面下滑沿圆弧上升,再滑回,这样往复运动,最后停在B点.已知质点与斜面间的动摩擦因数为μ=
如图所示,倾角θ=30°、长L=2.7m的斜面,底端与一个光滑的1/4圆弧平滑连接,圆弧底端切线水平.一个质量为m=1kg的质点从斜面最高点A沿斜面下滑,经过斜面底端B恰好到达圆弧最高点C,又从圆弧滑回,能上升到斜面上的D点,再由D点由斜面下滑沿圆弧上升,再滑回,这样往复运动,最后停在B点.已知质点与斜面间的动摩擦因数为μ= 如图所示,倾角θ=30°的光滑斜面上水平放置一条L=0.2m长的导线PQ,两端以很软的导线通入,I=5A的电流,方向由P流向Q.当竖直方向有一个B=0.6T的匀强磁场时,PQ恰能静止,求:
如图所示,倾角θ=30°的光滑斜面上水平放置一条L=0.2m长的导线PQ,两端以很软的导线通入,I=5A的电流,方向由P流向Q.当竖直方向有一个B=0.6T的匀强磁场时,PQ恰能静止,求: (2012?闵行区二模)如图所示,倾角θ=30°的斜面固定在地面上,长为L、质量为m、粗细均匀、质量分布均匀的软绳AB置于斜面上,与斜面间动摩擦因数μ=
(2012?闵行区二模)如图所示,倾角θ=30°的斜面固定在地面上,长为L、质量为m、粗细均匀、质量分布均匀的软绳AB置于斜面上,与斜面间动摩擦因数μ=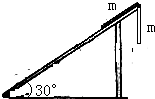 如图所示,倾角θ=30°的粗糙斜面固定在地面上,长为2l,质量为2m,粗细均匀,质量分布均匀的软绳,为黑色的一半置于斜面上,为白色一半悬在斜面外.软绳由静止释放后向下运动,直到软绳刚好全部离开斜面(此时下端未到达地面),在此过程中( )
如图所示,倾角θ=30°的粗糙斜面固定在地面上,长为2l,质量为2m,粗细均匀,质量分布均匀的软绳,为黑色的一半置于斜面上,为白色一半悬在斜面外.软绳由静止释放后向下运动,直到软绳刚好全部离开斜面(此时下端未到达地面),在此过程中( )