题目内容
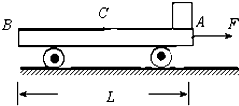 如图所示,光滑水平地面上停着一辆平板车,其质量为M(且M=3m),长为L,车右端(A点)有一块静止的质量为m的小金属块.金属块与车间有摩擦,以中点C为界,AC段与CB段摩擦因数不同.现给车施加一个向右的水平恒力,使车向右运动,同时金属块在车上开始滑动,当金属块滑到中点C时,立即撤去这个力.已知撤去力的瞬间,金属块的速度为v0,车的速度为2v0,最后金属块恰停在车的左端(B点).如果金属块与车的AC段间的动摩擦因数为μ1,与CB段间的动摩擦因数为μ2.
如图所示,光滑水平地面上停着一辆平板车,其质量为M(且M=3m),长为L,车右端(A点)有一块静止的质量为m的小金属块.金属块与车间有摩擦,以中点C为界,AC段与CB段摩擦因数不同.现给车施加一个向右的水平恒力,使车向右运动,同时金属块在车上开始滑动,当金属块滑到中点C时,立即撤去这个力.已知撤去力的瞬间,金属块的速度为v0,车的速度为2v0,最后金属块恰停在车的左端(B点).如果金属块与车的AC段间的动摩擦因数为μ1,与CB段间的动摩擦因数为μ2.(1)若μ1=0.3,m=1kg,求水平恒力F的大小;
(2)求μ1与μ2的比值.
分析:(1)隔离对m和M分析,根据牛顿第二定律,结合速度时间公式求出水平恒力F的大小.
(2)根据牛顿第二定律分别求出物块在CB段运动时,物块和小车的加速度,结合速度时间公式求出两者的共同速度,结合速度位移公式,抓住两者在AC段和BC段的位移之差都等于
求出动摩擦因数的比值.
(2)根据牛顿第二定律分别求出物块在CB段运动时,物块和小车的加速度,结合速度时间公式求出两者的共同速度,结合速度位移公式,抓住两者在AC段和BC段的位移之差都等于
| L |
| 2 |
解答:解:(1)由题意,物体在AC段滑动过程中,
对m:μ1mg=ma1
对M:F-μ1mg=3ma2
又v0=a1t
2v0=a2t
联立解得F=7μ1mg
代入数据得F=21N.
(2)设物块在CB段滑动的过程中,物块与木板的加速度分别为a1′和a2′,经历的时间为t′,则
在CB段:对m,μ2mg=ma1′
对M,μ2mg=3ma2′
又由运动学公式:v=v0+μ2gt′=2v0-a2′t′
解得v=
v0.
在CB段:
-
=
在AC段:
-
=
联立解得
=
.
答:(1)水平恒力F的大小为21N.
(2)μ1与μ2的比值为4:3.
对m:μ1mg=ma1
对M:F-μ1mg=3ma2
又v0=a1t
2v0=a2t
联立解得F=7μ1mg
代入数据得F=21N.
(2)设物块在CB段滑动的过程中,物块与木板的加速度分别为a1′和a2′,经历的时间为t′,则
在CB段:对m,μ2mg=ma1′
对M,μ2mg=3ma2′
又由运动学公式:v=v0+μ2gt′=2v0-a2′t′
解得v=
| 7 |
| 4 |
在CB段:
(2v0)2-(
| ||
| 2a2′ |
(
| ||
| 2a1 |
| L |
| 2 |
在AC段:
| (2v0)2 |
| 2a2 |
| v02 |
| 2a1 |
| L |
| 2 |
联立解得
| μ1 |
| μ2 |
| 4 |
| 3 |
答:(1)水平恒力F的大小为21N.
(2)μ1与μ2的比值为4:3.
点评:本题考查了牛顿第二定律和运动学公式的综合,加速度是联系运动学和力学的桥梁,结合两者的速度关系和位移关系,运用牛顿第二定律进行求解.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 滑块C离开A时的速度VC’
滑块C离开A时的速度VC’