题目内容
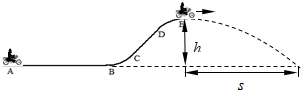
(2011?盐城一模)运动员驾驶摩托车做腾跃特技表演是一种刺激性很强的运动项目.如图所示,AB是水平路面,BC是半径为20m的圆弧,CDE是一段曲面.运动员驾驶功率始终是P=1.8kW的摩托车在AB段加速,到B点时速度达到最大υm=20m/s,再经t=13s的时间通过坡面到达E点时,关闭发动机后水平飞出.已知人和车的总质量m=180kg,坡顶高度h=5m,落地点与E点的水平距离s=16m,重力加速度g=10m/s2.如果在AB段摩托车所受的阻力恒定,求
(1)AB段摩托车所受阻力的大小;
(2)摩托车过B点时受到地面支持力的大小;
(3)摩托车在冲上坡顶的过程中克服阻力做功.
(1)AB段摩托车所受阻力的大小;
(2)摩托车过B点时受到地面支持力的大小;
(3)摩托车在冲上坡顶的过程中克服阻力做功.

分析:对人和车在B点分析,找出向心力的来源列出等式.
运用平抛运动规律求解平抛的初速度.
摩托车在斜坡上运动时,应用动能定理求出问题.
运用平抛运动规律求解平抛的初速度.
摩托车在斜坡上运动时,应用动能定理求出问题.
解答:解:(1)摩托车在水平面上已经达到了最大速度,牵引力与阻力相等.则
P=Fυ=fυ
f=
=90N
(2)摩托车在B点,进行受力分析,由牛顿第二定律得:N-mg=m
N=m
+mg=5400N
由牛顿第三定律得地面支持力的大小为5400N.
(3)对摩托车的平抛运动过程,有t=
=1s
平抛的初速度υ0=
=16m/s
摩托车在斜坡上运动时,由动能定理得Pt-Wf-mgh=
m
-
mυ2
求得Wf=27360J
答:(1)AB段摩托车所受阻力的大小是90N;
(2)摩托车过B点时受到地面支持力的大小是5400N;
(3)摩托车在冲上坡顶的过程中克服阻力做功是27360J.
P=Fυ=fυ
f=
| P |
| υ |
(2)摩托车在B点,进行受力分析,由牛顿第二定律得:N-mg=m
| υ2 |
| R |
N=m
| υ2 |
| R |
由牛顿第三定律得地面支持力的大小为5400N.
(3)对摩托车的平抛运动过程,有t=
|
平抛的初速度υ0=
| s |
| t |
摩托车在斜坡上运动时,由动能定理得Pt-Wf-mgh=
| 1 |
| 2 |
| υ | 2 0 |
| 1 |
| 2 |
求得Wf=27360J
答:(1)AB段摩托车所受阻力的大小是90N;
(2)摩托车过B点时受到地面支持力的大小是5400N;
(3)摩托车在冲上坡顶的过程中克服阻力做功是27360J.
点评:对于圆周运动分析关键要找到向心力的来源.
动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功.
一个题目可能需要选择不同的过程多次运用动能定理研究.
动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功.
一个题目可能需要选择不同的过程多次运用动能定理研究.

练习册系列答案
相关题目
 (2011?盐城一模)在2010年广州亚运会上,我国运动员陈一冰在吊环项目中取得了冠军.如图是比赛中的一个场景,此时人静止不动,两根吊带对称并与竖直方向有一定夹角.下列判断正确的是( )
(2011?盐城一模)在2010年广州亚运会上,我国运动员陈一冰在吊环项目中取得了冠军.如图是比赛中的一个场景,此时人静止不动,两根吊带对称并与竖直方向有一定夹角.下列判断正确的是( ) (2011?盐城一模)如图所示,斜面体M放置在水平地面上,位于斜面上的物块m受到沿斜面向上的推力F作用.设物块与斜面之间的摩擦力大小为F1,斜面与地面之间的摩擦力大小为F2.增大推力F,斜面体始终保持静止,下列判断正确的是( )
(2011?盐城一模)如图所示,斜面体M放置在水平地面上,位于斜面上的物块m受到沿斜面向上的推力F作用.设物块与斜面之间的摩擦力大小为F1,斜面与地面之间的摩擦力大小为F2.增大推力F,斜面体始终保持静止,下列判断正确的是( )


 (2011?盐城一模)如图所示,宽度L=1.0m的光滑金属框架MNPQ固定于水平面内,以M为坐标原点,MN方向为x轴正方向建立坐标系,x、y轴与虚线所包围的有界匀强磁场磁感应强度大小B=0.5T,方向竖直向下.现将质量m=0.1kg的金属棒ab放在框架上,与y轴重合,受到F=0.7N的力作用后,由静止沿x轴方向运动,经0.5s通过AB,接着一直做a=2m/s2的匀加速直线运动.PM段电阻为1Ω,其它部分电阻不计.求
(2011?盐城一模)如图所示,宽度L=1.0m的光滑金属框架MNPQ固定于水平面内,以M为坐标原点,MN方向为x轴正方向建立坐标系,x、y轴与虚线所包围的有界匀强磁场磁感应强度大小B=0.5T,方向竖直向下.现将质量m=0.1kg的金属棒ab放在框架上,与y轴重合,受到F=0.7N的力作用后,由静止沿x轴方向运动,经0.5s通过AB,接着一直做a=2m/s2的匀加速直线运动.PM段电阻为1Ω,其它部分电阻不计.求