题目内容
（2013?厦门模拟）如图所示，ABC为与匀强磁场垂直的边长为a的等边三角形，比荷为e/m的电子以速度v0从A 点沿AB边入射，欲使电子经过BC边，磁感应强度B的取值为（ ）分析：电子进入磁场后受到洛伦兹力作用而做匀速圆周运动，由半径公式r=
知，电子的速率越大，轨迹半径越大，欲使电子能经过BC边，当电子恰好从C点离开时，轨迹半径最小，由几何知识求出最小的半径，由半径公式求出B的最大值，即可得到B的范围．
| mv |
| qB |
解答：解：当电子从C点离开磁场时，电子做匀速圆周运动对应的半径最小，设为R，则几何知识得：
2Rcos30°=a，得R=
；
欲使电子能经过BC边，必须满足R＞
而R=
=
所以
＞
化简得B＜
；
故D正确，A、B、C错误．
故选：D
2Rcos30°=a，得R=
| a | ||
|
欲使电子能经过BC边，必须满足R＞
| a | ||
|
而R=
| mv0 |
| qB |
| mv0 |
| eB |
所以
| mv0 |
| eB |
| a | ||
|
化简得B＜
| ||
| ae |
故D正确，A、B、C错误．
故选：D
点评：本题是磁场中临界条件问题，关键是运用几何知识求最小的轨迹半径，即可由半径求解B的范围．
练习册系列答案
阅读快车系列答案
相关题目
（2013?厦门模拟）如图，在xOy平面内有一列沿x轴正方向传播的简谐横波，振幅为0.1m，频率为2.5Hz．在t=0时，平衡位置坐标x=2m的质点P点正经过平衡位置向下，平衡位置坐标x=5m的质点Q点位于波谷，且PQ之间只有一波峰，则下列说法正确的是（ ）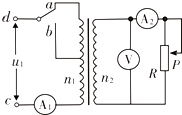
（2013?厦门模拟）如图所示，理想变压器原副线圈的匝数比为10：1，b是原线圈的中心抽头，电压表和电流表均为理想电表，除R 外其余电阻不计．在原线圈c、d两端加上u1=220
（2013?厦门模拟）将一弹性绳（质量不计）一端固定在某一高处O点，另一端系在一个物体上，现将物体从O点处由静止释放，测出物体在不同时刻的速度v和到O点的距离s，得到v-s图象如图所示．已知物体质量为5kg，弹性绳的自然长度为12m，（弹性绳的伸长在弹性限度内，遵循胡克定律，不计空气阻力，重力加速度g取10m/s2），则可知（ ）