题目内容
18.一支步枪的发射速度为v0,有人每一秒钟竖直向上打一枪,若不计阻力则第一颗子弹射出后与第n(n≥2)颗射出的子弹彼此相遇的时间为$\frac{{v}_{0}}{g}$+$\frac{n-1}{2}$(设子弹不相碰,且都在空中运动).分析 分析第一个小球和第n个小球的运动过程,明确在什么状态下能相撞;再由运动学公式列式求解即可.
解答 解:因为后面的子弹不会在第1颗上升过程中就超越第1颗子弹,也不可能2颗子弹都在下落时超越,所以只可能第一颗子弹在下降,而第n颗子弹在上升因为阻力是不计的,所以它们相遇时的速度大小一定相同;设相遇时的速度大小为v,所以第一颗子弹用时为:
t=$\frac{v}{g}$+$\frac{{v}_{0}}{g}$
第n颗子弹用时为:
t=n-1+$\frac{{v}_{0}}{g}$-$\frac{v}{g}$
联立求得:v$\frac{g(n-1)}{2}$,
所以有:t=$\frac{{v}_{0}}{g}$+$\frac{n-1}{2}$
故答案为:$\frac{{v}_{0}}{g}$+$\frac{n-1}{2}$
点评 本题考查竖直上抛运动问题,要注意明确所有小球在空中运动的过程均是相同的,要注意找出它们的联系.

练习册系列答案
相关题目
8.下列说法正确的是( )
| A. | 在匀速直线运动中,平均速度和瞬时速度相等 | |
| B. | 运动的物体受到的摩擦力一定是滑动摩擦力 | |
| C. | 摩擦力既可能使物体减速,也可能使物体加速 | |
| D. | 速度为零,物体一定处在平衡状态. |
9. 如图所示,A球用线悬挂且通过弹簧与B球相连,两球质量相等,当两球都静止时,将悬线烧断,不计空气阻力,下列说法正确的是( )
如图所示,A球用线悬挂且通过弹簧与B球相连,两球质量相等,当两球都静止时,将悬线烧断,不计空气阻力,下列说法正确的是( )
 如图所示,A球用线悬挂且通过弹簧与B球相连,两球质量相等,当两球都静止时,将悬线烧断,不计空气阻力,下列说法正确的是( )
如图所示,A球用线悬挂且通过弹簧与B球相连,两球质量相等,当两球都静止时,将悬线烧断,不计空气阻力,下列说法正确的是( )| A. | 线断瞬间,A球的加速度大于B球的加速度 | |
| B. | 线断后最初一段时间里,重力势能转化为动能和弹性势能 | |
| C. | 在下落过程中,两小球、弹簧和地球组成的系统机械能守恒 | |
| D. | 线断后最初一段时间里,动能增加大于重力势能的减小 |
6.为了防止静电危害,以下措施不正确的是( )
| A. | 油罐车有一条拖在地上的铁链 | |
| B. | 飞机机轮上装有搭地线,或用导电橡胶做轮胎 | |
| C. | 在地毯中夹杂不锈钢纤维 | |
| D. | 尽可能保持印染厂空气的干燥 |
3.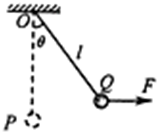 如图所示,一质量为m的小球,用长为L的轻绳悬挂于O点,初始时刻小球静止于P点,第一次小球在水平拉力F作用下,从P点缓慢地移动到Q点,此时轻绳与竖直方向夹角为θ,张力大小为T1,第二次在水平恒力F′作用下,从P点开始运动并恰好能到达Q点,至Q点时轻绳中的张力大小为T2,不计空气阻力,重力加速度为g,关于这两个过程,下列说法中正确的是( )
如图所示,一质量为m的小球,用长为L的轻绳悬挂于O点,初始时刻小球静止于P点,第一次小球在水平拉力F作用下,从P点缓慢地移动到Q点,此时轻绳与竖直方向夹角为θ,张力大小为T1,第二次在水平恒力F′作用下,从P点开始运动并恰好能到达Q点,至Q点时轻绳中的张力大小为T2,不计空气阻力,重力加速度为g,关于这两个过程,下列说法中正确的是( )
 如图所示,一质量为m的小球,用长为L的轻绳悬挂于O点,初始时刻小球静止于P点,第一次小球在水平拉力F作用下,从P点缓慢地移动到Q点,此时轻绳与竖直方向夹角为θ,张力大小为T1,第二次在水平恒力F′作用下,从P点开始运动并恰好能到达Q点,至Q点时轻绳中的张力大小为T2,不计空气阻力,重力加速度为g,关于这两个过程,下列说法中正确的是( )
如图所示,一质量为m的小球,用长为L的轻绳悬挂于O点,初始时刻小球静止于P点,第一次小球在水平拉力F作用下,从P点缓慢地移动到Q点,此时轻绳与竖直方向夹角为θ,张力大小为T1,第二次在水平恒力F′作用下,从P点开始运动并恰好能到达Q点,至Q点时轻绳中的张力大小为T2,不计空气阻力,重力加速度为g,关于这两个过程,下列说法中正确的是( )| A. | 两个过程中,轻绳的张力均变大 | |
| B. | 第一个过程中,拉力F在逐渐变大,且最大值一定大于F′ | |
| C. | T1=$\frac{mg}{cosθ}$,T2=mg | |
| D. | 第二个过程中,重力和水平恒力F′的合力的功率先增大后减小 |
1.下列哪个选项说法正确( )
| A. | +q在A点的电势能比在B点大,则B点的电势高 | |
| B. | -q在C点的电势能比在D点大,则C点的电势高 | |
| C. | +q在E点的电势能为负值,-q在F点的电势能为负值,则F点的电势高 | |
| D. | 以上说法都不正确 |
 如图所示,水平轨道AB与竖直半圆轨道BD相切于B点,半圆轨道的半径为R,整个轨道处于竖直向下的电场强度为E的匀强电场中.一个质量为m,带电量为+q的小球从水平
如图所示,水平轨道AB与竖直半圆轨道BD相切于B点,半圆轨道的半径为R,整个轨道处于竖直向下的电场强度为E的匀强电场中.一个质量为m,带电量为+q的小球从水平