题目内容
一矿井深为125 m,在井口每隔一段时间落下一小球,当第十一个小球刚好从井口开始下落时,第一个小球恰好到达井底,相邻两个小球开始下落的时间间隔是多少?此时第三个小球和第五个小球相距多远?
0.5 s 35 m
把11个小球看做是1个小球的自由落体运动,则从第十一个小球刚离开井口的时刻算起,通过相等的时间间隔内各相邻小球的间距之比为
ΔsⅠ：ΔsⅡ：ΔsⅢ：…：ΔsN=1：3：5：…：(2n-1)
n=10,
则Δs1=
="1.25" m
ΔsⅡ=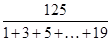
×3="3.75" m
根据Δs=gT2
所以,相邻两个小球下落时间间隔为
ΔT=
="0.5" s
此时第三个小球与第五个小球相距
s=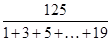×(13+15)="35" m.
ΔsⅠ：ΔsⅡ：ΔsⅢ：…：ΔsN=1：3：5：…：(2n-1)
n=10,
则Δs1=
="1.25" mΔsⅡ=
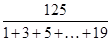×3="3.75" m根据Δs=gT2
所以,相邻两个小球下落时间间隔为
ΔT=
="0.5" s此时第三个小球与第五个小球相距
s=
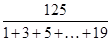×(13+15)="35" m.
练习册系列答案
全程金卷系列答案
快乐5加2金卷系列答案
相关题目