题目内容
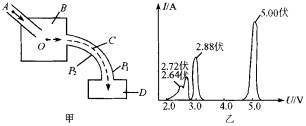
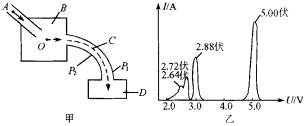
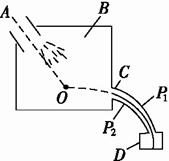
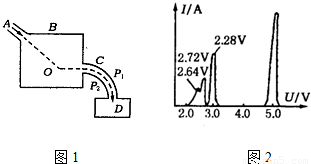
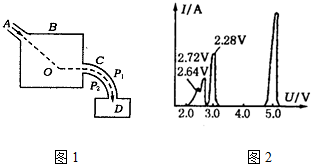
如图1是证实玻尔关于原子存在分立能态的一种实验装置的原理示意图.由电子枪A射出的电子,射进一容器B中,其中有氦气.电子在O点与氦原子发生碰撞后进入速度选择器C,然后进入检测装置D.速度选择器C由两个同心的圆弧形电极P1和P2组成.当两极间加以电压U时,只允许具有确定能量的电子通过,并进入检测装置D,由检测装置测出电子产生的电流I.改变电压U,同时测出I的数值,即可确定碰撞后进入速度选择器的电子的能量分布.为简单起见,设电子与原子碰撞前,原子是静止的,原子质量比电子质量大得多,碰撞后,原子虽然稍微被碰动,但忽略这一能量损失,设原子未动,当电子与原子发生了弹性碰撞时,电子改变运动方向,但不损失动能,当发生非弹性碰撞时,电子损失的动能传给原子,使原子内部的能量增大.(1)设速度选择器两极间的电压为U(V)时,允许通过的电子的动能为Ek(eV),试求出Ek(eV)与U(V)的函数关系.设通过选择器的电子的轨道半径r=20.0cm,电极P1和P2的间隔d=1.00cm,两极间场强的大小处处相等.
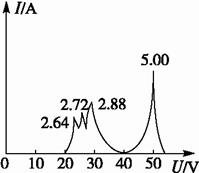
(2)当电子枪射出电子的动能Ek0=50.0eV时,改变电压U(V),测出电流I(A),得到如图2所示图线,图线表示,当电压U为5.00V,2.88V,2.72V,2.64V时,电流出现峰值.先定性说明图二表示的物理意义,根据实验结果求出氦原子三个激发态的能级En(eV),设基态的能级E1=0eV.
【答案】分析:一定的速度v的电子在速度选择器的两极间做匀速圆周运动,向心力是由电场力提供的,列出等式求解.
原子存在分立的能态,即定态的存在,根据能量守恒求解.
解答:解:(1)当两极间的电压为U(V)时,具有一定的速度v的电子在速度选择器的两极间做匀速圆周运动,向心力是由电场力提供的,设电子质量为m,电子电量为e,电子所受电场力为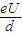 ,由此得电子的动能Ek=
,由此得电子的动能Ek= mv2=
mv2=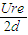 =10.0U(eV),
=10.0U(eV),
这表明,当两极间的电压为U(V)时,允许通过的动能为10.0U(eV)的电子,大于和小于10.0U(eV)的电子将分别落在两极上,而不能达检测装置D.
(2)电压为5.0V时有峰值,表示动能为50.0eV的电子通过选择器,即有碰撞后动能为50.0V的电子.这与入射电子的动能相同,电子与氦原子发生弹性碰撞,电压为4.0V时没有电流,这表明碰撞后没有动能为40.0的电子,即在非弹性碰撞中,电子的动能不可能只损失(50.0-40.0)eV=10.0eV,也就是说氦原子不接受10.0eV的能量,电压为2.88V、2.72V、2.64V时有峰值,分别表示有碰撞后动能为28.8V、27.2V、26.4V的电子,氦原子接受电子在非弹性碰撞中损失的动能,这个实验说明了原子存在分立的能态,即定态的存在.
在该氢原子激发态的能级为En,
则从实验结果可知En的数值为:(50.0-28.8)eV=21.2eV,(50.0-27.2)eV=22.8eV,(50.0-26.4)eV=23.6eV
答:(1)Ek(eV)与U(V)的函数关系是Ek=10.0U(eV),
(2)氦原子三个激发态的能级是21.2eV,22.8eV,23.6eV
点评:解决本题的关键掌握能级间跃迁辐射的光子频率与能级差的关系.
原子存在分立的能态,即定态的存在,根据能量守恒求解.
解答:解:(1)当两极间的电压为U(V)时,具有一定的速度v的电子在速度选择器的两极间做匀速圆周运动,向心力是由电场力提供的,设电子质量为m,电子电量为e,电子所受电场力为
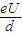 ,由此得电子的动能Ek=
,由此得电子的动能Ek= mv2=
mv2=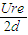 =10.0U(eV),
=10.0U(eV),这表明,当两极间的电压为U(V)时,允许通过的动能为10.0U(eV)的电子,大于和小于10.0U(eV)的电子将分别落在两极上,而不能达检测装置D.
(2)电压为5.0V时有峰值,表示动能为50.0eV的电子通过选择器,即有碰撞后动能为50.0V的电子.这与入射电子的动能相同,电子与氦原子发生弹性碰撞,电压为4.0V时没有电流,这表明碰撞后没有动能为40.0的电子,即在非弹性碰撞中,电子的动能不可能只损失(50.0-40.0)eV=10.0eV,也就是说氦原子不接受10.0eV的能量,电压为2.88V、2.72V、2.64V时有峰值,分别表示有碰撞后动能为28.8V、27.2V、26.4V的电子,氦原子接受电子在非弹性碰撞中损失的动能,这个实验说明了原子存在分立的能态,即定态的存在.
在该氢原子激发态的能级为En,
则从实验结果可知En的数值为:(50.0-28.8)eV=21.2eV,(50.0-27.2)eV=22.8eV,(50.0-26.4)eV=23.6eV
答:(1)Ek(eV)与U(V)的函数关系是Ek=10.0U(eV),
(2)氦原子三个激发态的能级是21.2eV,22.8eV,23.6eV
点评:解决本题的关键掌握能级间跃迁辐射的光子频率与能级差的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图1是证实玻尔关于原子存在分立能态的一种实验装置的原理示意图.由电子枪A射出的电子,射进一容器B中,其中有氦气.电子在O点与氦原子发生碰撞后进入速度选择器C,然后进入检测装置D.速度选择器C由两个同心的圆弧形电极P1和P2组成.当两极间加以电压U时,只允许具有确定能量的电子通过,并进入检测装置D,由检测装置测出电子产生的电流I.改变电压U,同时测出I的数值,即可确定碰撞后进入速度选择器的电子的能量分布.为简单起见,设电子与原子碰撞前,原子是静止的,原子质量比电子质量大得多,碰撞后,原子虽然稍微被碰动,但忽略这一能量损失,设原子未动,当电子与原子发生了弹性碰撞时,电子改变运动方向,但不损失动能,当发生非弹性碰撞时,电子损失的动能传给原子,使原子内部的能量增大.
如图1是证实玻尔关于原子存在分立能态的一种实验装置的原理示意图.由电子枪A射出的电子,射进一容器B中,其中有氦气.电子在O点与氦原子发生碰撞后进入速度选择器C,然后进入检测装置D.速度选择器C由两个同心的圆弧形电极P1和P2组成.当两极间加以电压U时,只允许具有确定能量的电子通过,并进入检测装置D,由检测装置测出电子产生的电流I.改变电压U,同时测出I的数值,即可确定碰撞后进入速度选择器的电子的能量分布.为简单起见,设电子与原子碰撞前,原子是静止的,原子质量比电子质量大得多,碰撞后,原子虽然稍微被碰动,但忽略这一能量损失,设原子未动,当电子与原子发生了弹性碰撞时,电子改变运动方向,但不损失动能,当发生非弹性碰撞时,电子损失的动能传给原子,使原子内部的能量增大.