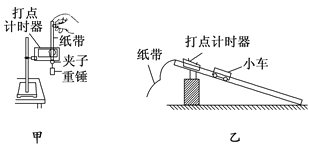
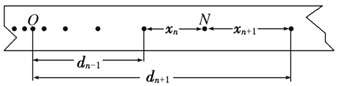
题目内容
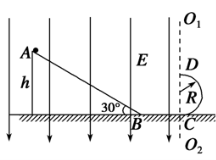
【题目】如图所示,竖直平面直角坐标系中,一半径为R的绝缘光滑管道位于其中,管道圆心坐标为(0,R),其下端点与x轴相切与坐标原点,其上端点与y轴交于C点,坐标为(0,2R)。在第二象限内,存在水平向右、范围足够大的匀强电场,电场强度大小为![]() ,在
,在![]() 范围内,有水平向左,范围足够大的匀强电场,电场强度大小为
范围内,有水平向左,范围足够大的匀强电场,电场强度大小为![]() 。现有一与x轴正方向夹角为45°,足够长的绝缘斜面位于第一象限的电场中,斜面底端坐标为(R,0),x轴上
。现有一与x轴正方向夹角为45°,足够长的绝缘斜面位于第一象限的电场中,斜面底端坐标为(R,0),x轴上![]() 范围内是水平光滑轨道,左端与管道下端相切,右端与斜面底端平滑连接,有一质量为m,带电量为+q的小球,从静止开始,由斜面上某点A下滑,通过水平光滑轨道(不计转角处能量损失),从管道下端点B进入管道(小球直径略小于管道内径,不计小球的电量损失)(已知重力加速度为g)。试求:
范围内是水平光滑轨道,左端与管道下端相切,右端与斜面底端平滑连接,有一质量为m,带电量为+q的小球,从静止开始,由斜面上某点A下滑,通过水平光滑轨道(不计转角处能量损失),从管道下端点B进入管道(小球直径略小于管道内径,不计小球的电量损失)(已知重力加速度为g)。试求:
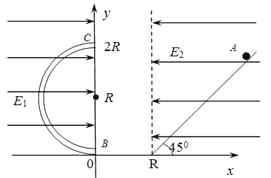
(1)小球至少从多高处滑下,才能到达管道上端点C?要求写出此时小球出发点的坐标;
(2)在此情况下,小球通过管道最高点C受到的压力多大?方向如何?
【答案】(1)![]() (2)
(2)![]() ,方向向上
,方向向上
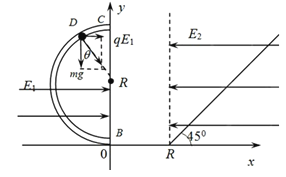
【解析】试题分析:(1)如图,在第二象限内,小球受到水平向右的电场力和竖直向下的重力,设两者合力与y轴夹角为![]() ,则:
,则:
![]() ,
,![]()
即带电小球所受重力和电场力的合力方向斜向右下方,与y轴夹角为300,将重力场与电场等效为新的场,等效重力加速度![]() .
.
分析可知,电场力和重力的合力作用线通过圆心时,合力作用线与管道的交点D处小球的速度最小,为vD=0.
先计算B点最小速度,从B点到D点,由动能定理有:![]()
得![]()
在第一象限的复合场中,分析可知,小球由静止开始,做匀加速运动,其等效加速度为![]()
所以,A点纵坐标![]() ,
,
A点横坐标![]() ,即
,即![]()
(2)从B点到C点,由动能定理有:![]() ,得
,得![]()
小球通过最高点C时,向心力由重力和管道压力提供,设管道对小球的作用力竖直向上,有:![]()
![]()
所以,管道对小球的压力大小为![]() ,方向向上.
,方向向上.