题目内容
 如图所示为氢原子能级示意图,现有每个电子的动能都是Ee=12.89eV的电子束与处在基态的氢原子束射入同一区域,使电子与氢原子发生迎头正碰.已知碰撞前一个电子和一个原子的总动量为零.碰撞后氢原子受激发,跃迁到n=4的能级.求碰撞后一个电子和一个受激氢原子的总动能.已知电子的质量me与氢原子的质量mH之比为
如图所示为氢原子能级示意图,现有每个电子的动能都是Ee=12.89eV的电子束与处在基态的氢原子束射入同一区域,使电子与氢原子发生迎头正碰.已知碰撞前一个电子和一个原子的总动量为零.碰撞后氢原子受激发,跃迁到n=4的能级.求碰撞后一个电子和一个受激氢原子的总动能.已知电子的质量me与氢原子的质量mH之比为| me | mH |
分析:根据动量守恒研究电子与氢原子发生碰撞列出等式,根据动能的表达式求出碰撞前一个电子和一个受激氢原子的总动能.
根据能量需要等于两能级间的能级差求出碰撞后一个电子和一个受激氢原子的总动能.
根据能量需要等于两能级间的能级差求出碰撞后一个电子和一个受激氢原子的总动能.
解答:解:以ve和vH表示碰撞前电子的速率和氢原子的速率,
根据题意有:me
-mH
=0
碰撞前,氢原子与电子的总动能为Ek=
mH
+
me
解以上两式并代入数据得:
Ek=12.897eV≈12.90eV
氢原子从基态激发到n=4的能级所需能量由能级图得△E=-0.85-(-13.59)=12.74eV
碰撞后电子和受激氢原子的总动能E'k=Ek-△E=12.90-12.74=0.16eV
答:碰撞后一个电子和一个受激氢原子的总动能是0.16eV
根据题意有:me
| v | e |
| v | H |
碰撞前,氢原子与电子的总动能为Ek=
| 1 |
| 2 |
| v | 2 H |
| 1 |
| 2 |
| v | 2 e |
解以上两式并代入数据得:
Ek=12.897eV≈12.90eV
氢原子从基态激发到n=4的能级所需能量由能级图得△E=-0.85-(-13.59)=12.74eV
碰撞后电子和受激氢原子的总动能E'k=Ek-△E=12.90-12.74=0.16eV
答:碰撞后一个电子和一个受激氢原子的总动能是0.16eV
点评:本题综合考查了动量守恒、能量守恒定律以及能级的跃迁,综合性较强,难度中等.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图所示为氢原子能级图,下列说法中正确的是( )
如图所示为氢原子能级图,下列说法中正确的是( )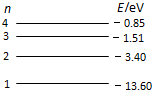 如图所示为氢原子能级图,一群氢原子处于n=3的激发态,在向较低能级跃迁的过程中向外发出光子,并用这些光照射逸出功为2.49eV的金属钠.
如图所示为氢原子能级图,一群氢原子处于n=3的激发态,在向较低能级跃迁的过程中向外发出光子,并用这些光照射逸出功为2.49eV的金属钠.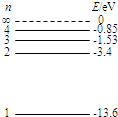 如图所示为氢原子能级图,可见光的光子能量范围约为1.62eV~3.11eV.下列说法正确的是( )
如图所示为氢原子能级图,可见光的光子能量范围约为1.62eV~3.11eV.下列说法正确的是( )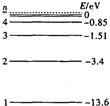 (1)如图所示为氢原子能级图,下列说法正确的是
(1)如图所示为氢原子能级图,下列说法正确的是