题目内容
13.做匀变速直线运动的物体,初速度为20m/s,方向沿x轴正方向,经过2s,末速度变为20m/s,方向沿x轴负方向.若规定以x轴正方向为正,则其加速度和2s内的平均速度分别是( )| A. | 20m/s2;0 | B. | 0;20m/s | C. | -20m/s2;0 | D. | -20m/s2;20m/s |
分析 根据加速度的定义式a=$\frac{△v}{△t}$求出加速度,平均速度根据$\overline{v}=\frac{{v}_{0}+v}{2}$即可求解.
解答 解:根据加速度的定义式a=$\frac{△v}{△t}$得:
a=$a=\frac{-20-20}{2}=-20m/{s}^{2}$
2s内的平均速度为:$\overline{v}=\frac{{v}_{0}+v}{2}=\frac{20+(-20)}{2}=0$
故选:C
点评 本题关键考查匀变速直线运动的速度时间关系和位移时间关系,注意速度的矢量性即可.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
3.一物块从某一高度水平抛出,刚抛出时其动能与重力势能恰好相等(取水平地面作为参考平面).不计空气阻力,该物块落地时的速度方向与水平方向的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
4.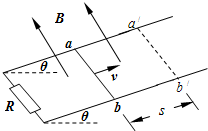 如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达虚线a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达虚线a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
 如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达虚线a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达虚线a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )| A. | 上滑过程中导体棒受到的最大安培力为$\frac{{B}^{2}{l}^{2}v}{R}$ | |
| B. | 上滑过程中导体棒损失的机械能大小为μmgs cosθ | |
| C. | 上滑过程中电流做功发出的热量为$\frac{m{v}^{2}}{2}$-mgs (sinθ+μcosθ) | |
| D. | 上滑过程中安培力、滑动摩擦力和重力对导体棒做的总功为正$\frac{m{v}^{2}}{2}$ |
5.下列选项中可以和能量单位等效对应的是( )
| A. | N•m/s | B. | N•m/s2 | C. | kg•(m/s)2 | D. | kg.m/s2 |
2.发现万有引力定律的物理学家是( )
| A. | 开普勒 | B. | 牛顿 | C. | 卡文迪许 | D. | 伽利略 |
 在做用油膜法估测分子大小的实验中,已知实验室中使用的油酸酒精溶液的体积浓度为A,又用滴管测得N滴这种油酸酒精的总体积为V,将一滴这种溶液滴在浅盘中的水面上,在玻璃板上描出油膜的边界线,再把玻璃板放在画有边长为a的正方形小格的纸上,如图所示,测得油膜占有的小正方形个数为X.用以上字母表示油酸分子直径的大小d=$\frac{VA}{NX{a}^{2}}$.
在做用油膜法估测分子大小的实验中,已知实验室中使用的油酸酒精溶液的体积浓度为A,又用滴管测得N滴这种油酸酒精的总体积为V,将一滴这种溶液滴在浅盘中的水面上,在玻璃板上描出油膜的边界线,再把玻璃板放在画有边长为a的正方形小格的纸上,如图所示,测得油膜占有的小正方形个数为X.用以上字母表示油酸分子直径的大小d=$\frac{VA}{NX{a}^{2}}$.