题目内容
一个电荷量为-q,质量为m的小球,从光滑绝缘的斜面轨道的A点由静止下滑,小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动。现在竖直方向上加如图所示的匀强电场,且电场强度满足mg=2qE,若仍从A点由静止释放该小球,则( )
| A.小球仍恰好能过B点 |
| B.小球不能过B点 |
| C.小球能过B点,且在B点与轨道之间压力不为零 |
D.小球到达B点的速度 |
AD
解析试题分析:没有电场时,最高点速度设为v; 则 mg=m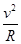 ;又根据机械能守恒定律
;又根据机械能守恒定律
mg(h-2R)=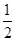 mv2 ;解得h=
mv2 ;解得h=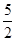 R
R
加上电场时,恰好过最高点需要的速度设为v′,则mg-qE=m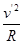 ,
, 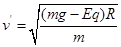
而由动能定理,得mg(h-2R)-qE(h-2R)=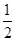 mv′2,解得:
mv′2,解得: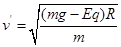
说明小球仍恰好能过B点.故A正确,B错误.由以上分析可知,小球仍恰好过最高点,球与轨道间无作用力.故C错误;由于mg=2qE,所以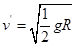 ,选项D正确。
,选项D正确。
考点:动能定理及牛顿定律的应用。

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案如图甲所示,轻质弹簧的下端固定在水平面上,上端放置一小物体(物体与弹簧不连接),初始时物体处于静止状态。现用竖直向上的拉力F作用在物体上,使物体开始向上做匀加速直线运动,拉力F与物体位移x的关系如图乙所示(g=10m/s2),则下列结论正确的是( )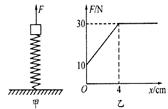
| A.物体与弹簧分离时,弹簧处于压缩状态 |
| B.物体的质量为3 kg |
| C.物体的加速度大小为5 m/s2 |
| D.弹簧的劲度系数为7. 5 N/cm |
跳伞运动员从悬停的直升机上跳下,经过一段时间后开启降落伞。如图所示是跳伞过程中的v-t图象。若将人和伞看成一个系统,则以下认识正确的是
| A.系统先加速下降,接着减速上升 |
| B.系统受到的合外力始终向下 |
| C.阻力对系统始终做负功 |
| D.系统的机械能守恒 |
静止在光滑水平面上的物体,突然受到一个如图所示的水平外力的作用,则
| A.物体沿水平面做往复运动 |
| B.物体始终沿水平面朝一个方向运动 |
| C.物体沿水平面先做匀加速运动,后做匀减速运动 |
| D.物体沿水平面一直做匀加速运动 |
“蹦极”就是跳跃者把一端固定的长弹性绳绑在踝关节等处,从几十米高处跳下的一种极限运动。某人做蹦极运动,所受绳子拉力F的大小随时间t变化的情况如图所示。将蹦极过程近似为在竖直方向的运动,重力加速度为g。据图可知,此人在蹦极过程中最大加速度约为
| A.g | B.2g | C.3g | D.4g |
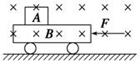
如图所示,质量形状均相同的木块紧靠在一起,放在光滑的水平面上,现用水平恒力F推1号木块,使10个木块一起向右匀加速运动,则第6号对第7号木块的推力为( ) 
| A.F | B.0.8F | C.0.4F | D.0.2F |
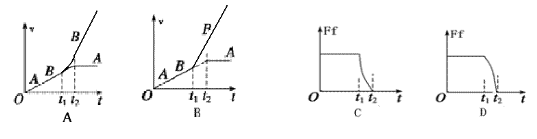

 的斜面底端,另一端与物块A连接,物块B沿斜面叠放在物块A上但不黏连。物块A、B质量均为m,初始时两物块均静止。现用平行于斜面向上的拉力F拉动物块B,使B做加速度为a的匀加速运动,两物块在开始一段时间内的v-t图象如图乙所示(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,则
的斜面底端,另一端与物块A连接,物块B沿斜面叠放在物块A上但不黏连。物块A、B质量均为m,初始时两物块均静止。现用平行于斜面向上的拉力F拉动物块B,使B做加速度为a的匀加速运动,两物块在开始一段时间内的v-t图象如图乙所示(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,则 


 时A、B分离
时A、B分离