题目内容
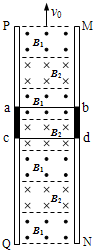
如图所示是一种磁动力电梯的模拟机,即在竖直平面内有两根很长的平行竖直轨道,轨道间有垂直轨道平面的匀强磁场B1和B2,且B1和B2的方向相反,B1=B2=1T,电梯桥厢固定在如图所示的一个用超导材料制成的金属框abcd内(电梯桥厢在图中未画出),并且与之绝缘.电梯载人时的总质量为m=5×103 kg,所受阻力大小为Ff=500 N,金属框垂直轨道的边长为Lcd=2 m,两磁场的宽度均与金属框的边长Lac相同,金属框整个回路的电阻为R=1.0×10-3 Ω,问:
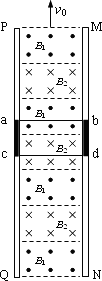
(1)假如两磁场始终竖直向上做匀速运动.设计要求电梯以v1=10 m/s的速度向上匀速运动,那么,磁场向上运动的速度v0应该为多大?
(2)假如t=0时两磁场由静止开始向上做匀加速运动,加速度大小为a=1.5 m/s2,电梯可近似认为过一小段时间后也由静止开始向上做匀加速运动,t=5 s末电梯的速度多大?电梯运动的时间内金属框中消耗的电功率多大?从电梯开始运动到t=5 s末时间内外界提供给系统的总能量为多大?
解析:
|
(1)电梯向上匀速运动时,框中感应电流大小为I=2B1Lcd(v0-v1)/R(1分), 金属框所受安培力F=2B1ILcd(1分), 安培力大小与重力和阻力之和相等,所以F=mg+Ff(1分), 即4B12Lcd2(v0-v1)/R=mg+Ff(2分),可得:v0=13.2 m/s(1分), (2)电梯向上匀加速运动时,金属框中感应电流大小为I=2B1Lcd(v2-v1)/R(1分), 金属框所受安培力F=2B1ILcd,由牛顿定律得:F-mg-Ff=ma(1分), 即4B12Lcd2(at-v1)/R-mg-Ff=ma(1分), 解得:v1=at-(mg+ma+Ff)R/4B12Lcd2=3.9 m/s(1分), 金属框中感应电流为:I=2B1Lcd(at-v1)/R=1.44×104 A(1分), 金属框中的电功率为:P1=I2R=2.07×105 W(1分), 电梯上升高度为h=v12/2a=5.07 m(1分),上升时间为 外界提供的总能量为E=mgh+Ffh+ |

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案 如图所示是一种磁动力电梯的模拟机,即在竖直平面内有两根很长的平行竖直轨道,轨道间有垂直轨道平面的匀强磁场B1和B2,且B1和B2的方向相反,B1=B2=1T,电梯桥厢固定在如图所示的一个用超导材料制成的金属框abcd内(电梯桥厢在图中未画出),并且与之绝缘.电梯载人时的总质量为m=5×103kg,所受阻力大小为Ff=500N,金属框垂直轨道的边长为Lcd=2m,两磁场的宽度均与金属框的边长Lac相同,金属框整个回路的电阻为R=1.0×10-3Ω,问:
如图所示是一种磁动力电梯的模拟机,即在竖直平面内有两根很长的平行竖直轨道,轨道间有垂直轨道平面的匀强磁场B1和B2,且B1和B2的方向相反,B1=B2=1T,电梯桥厢固定在如图所示的一个用超导材料制成的金属框abcd内(电梯桥厢在图中未画出),并且与之绝缘.电梯载人时的总质量为m=5×103kg,所受阻力大小为Ff=500N,金属框垂直轨道的边长为Lcd=2m,两磁场的宽度均与金属框的边长Lac相同,金属框整个回路的电阻为R=1.0×10-3Ω,问: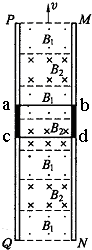 如图所示是一种磁动力电梯的模拟机,即在竖直平面上有两根很长的平行竖直轨道,轨道间有垂直轨道平面的匀强磁场B1和B2,且B1和B2的方向相反,大小相等,即B1=B2=1T,两磁场始终竖直向上作匀速运动.电梯桥厢固定在如图所示的一个用超导材料制成的金属框abcd内(电梯桥厢在图中未画出),并且与之绝缘.电梯载人时的总质量为750kg,所受阻力f=500N,金属框垂直轨道的边长Lcd=2m,两磁场的宽度均与金属框的边长Lac相同,金属框整个回路的电阻R=6×10-3Ω,假如设计要求电梯以v1=10m/s的速度向上匀速运动,那么,
如图所示是一种磁动力电梯的模拟机,即在竖直平面上有两根很长的平行竖直轨道,轨道间有垂直轨道平面的匀强磁场B1和B2,且B1和B2的方向相反,大小相等,即B1=B2=1T,两磁场始终竖直向上作匀速运动.电梯桥厢固定在如图所示的一个用超导材料制成的金属框abcd内(电梯桥厢在图中未画出),并且与之绝缘.电梯载人时的总质量为750kg,所受阻力f=500N,金属框垂直轨道的边长Lcd=2m,两磁场的宽度均与金属框的边长Lac相同,金属框整个回路的电阻R=6×10-3Ω,假如设计要求电梯以v1=10m/s的速度向上匀速运动,那么,