题目内容
2.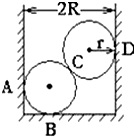 如图,两只相同的均匀光滑小球置于半径为R=18cm的圆柱形容器中,且小球的半径r=10cm,小球的质量为2Kg,求:容器底B处对球的支持力和容器壁A处对球的弹力各是多少?(g=10m/s2)
如图,两只相同的均匀光滑小球置于半径为R=18cm的圆柱形容器中,且小球的半径r=10cm,小球的质量为2Kg,求:容器底B处对球的支持力和容器壁A处对球的弹力各是多少?(g=10m/s2)
分析 对整体受力分析,整体处于平衡状态,可得出容器底面对A球的弹力大小,以及容器左壁对A球的弹力与容器右壁对B球的弹力的关系.再隔离对B球受力分析,可知两球间的弹力大小跟球重力的大小关系.
解答  解:以两球为系统,这系统受的外力:G总=2mg,NB 为容器底对系统支持力,NA,ND为容器壁对系统弹力.
解:以两球为系统,这系统受的外力:G总=2mg,NB 为容器底对系统支持力,NA,ND为容器壁对系统弹力.
这四力平衡:ND=NA
NB=G总=2mg=40N
以底部球为对象:NC为另一个球对它弹力
NA=$\frac{{N}_{B}-G}{tanθ}$
在三角形0102P中:01P=2R-2r=2×18-2×10=16cm
O2P=$\sqrt{{O}_{1}{O}_{2}^{2}-{O}_{1}{P}^{2}}$=$\sqrt{2{0}^{2}-1{6}^{2}}$cm=12cm
则 tanθ=$\frac{{O}_{2}P}{{O}_{1}P}$=$\frac{12}{16}$=$\frac{3}{4}$
代入数据得:NA=$\frac{80}{3}$N
答:容器底B处对球的支持力和容器壁A处对球的弹力各是40N和$\frac{80}{3}$N.
点评 该题运用了整体法和隔离法,对整体分析,可得出容器底面的弹力的大小和左右两侧的弹力大小关系.

练习册系列答案
相关题目
8.关于运动的合成,下列说法中正确的是( )
| A. | 合运动的速度一定比每一个分运动的速度大 | |
| B. | 两个不在一直线上的匀速直线运动的合运动一定是匀速直线运动 | |
| C. | 两个匀变速直线运动的合运动不一定是匀变速直线运动 | |
| D. | 合运动的两个分运动的时间不一定相等 |
9.以下是有关近代物理内容的若干叙述,其中正确的有( )
| A. | 有10个放射性元素的原子核,当有5个原子核发生衰变所需的时间就是该放射性元素的半衰期 | |
| B. | 用α粒子轰击铍核(${\;}_{4}^{9}$Be),可以得到碳核(${\;}_{6}^{12}$C)和质子 | |
| C. | 氢原子的核外电子由较高能级迁到较低能级时,要释放一定频率的光子,同时电子的动能增大,电势能减小 | |
| D. | 用γ射线治疗肿瘤时一定要严格控制剂量,以免对人体正常组织造成太大的伤害 |
10. 如图所示,在竖直平面内的固定光滑元轨道的最高点有一个光滑的小孔,质量为m的小环套在圆轨道上,用细线通过小孔系在环上,缓慢 拉动细线,使环沿轨道上移,在移动过程中拉力F和轨道对小环的作用力FN的大小变化情况是( )
如图所示,在竖直平面内的固定光滑元轨道的最高点有一个光滑的小孔,质量为m的小环套在圆轨道上,用细线通过小孔系在环上,缓慢 拉动细线,使环沿轨道上移,在移动过程中拉力F和轨道对小环的作用力FN的大小变化情况是( )
 如图所示,在竖直平面内的固定光滑元轨道的最高点有一个光滑的小孔,质量为m的小环套在圆轨道上,用细线通过小孔系在环上,缓慢 拉动细线,使环沿轨道上移,在移动过程中拉力F和轨道对小环的作用力FN的大小变化情况是( )
如图所示,在竖直平面内的固定光滑元轨道的最高点有一个光滑的小孔,质量为m的小环套在圆轨道上,用细线通过小孔系在环上,缓慢 拉动细线,使环沿轨道上移,在移动过程中拉力F和轨道对小环的作用力FN的大小变化情况是( )| A. | F不变,FN增大 | B. | F不变,FN不变 | C. | F减小,FN不变 | D. | F增大,FN增大 |
7.一小球做加速直线运动,在第1s内通过1m,在第2s内通过2m,在第3s内通过3m,在第4s内通过4m.下面有关小球的运动情况的描述中,错误的一项是( )
| A. | 小球在这4s内的平均速度是2.5m/s | |
| B. | 小球在第3s和第4s这两秒内的平均速度是3.5 m/s | |
| C. | 小球在这4s内可能做初速度为零的匀加速直线运动 | |
| D. | 小球在这4s内的加速度可能为1m/s2 |
14.如图所示的s-t图象和v-t图象中,给出的四条曲线1、2、3、4,分别代表四个不同物体的运动情况,关于它们的物理意义,下列描述正确的是( )


| A. | 曲线1表示物体做曲线运动 | |
| B. | s-t图象中,t1时刻v1>v2 | |
| C. | v-t图象中0至t3时间内物体3和物体4的平均速度大小相等 | |
| D. | 两图象中,t2、t4时刻分别表示物体2、4开始反向运动 |
12. 将一单摆向左拉至水平标志线上,从静止释放,当摆球运动到最低点时,摆线碰到障碍物,摆球继续向右摆动.用频闪照相机拍到如图所示的单摆运动过程的频闪照片,以下说法正确的是( )
将一单摆向左拉至水平标志线上,从静止释放,当摆球运动到最低点时,摆线碰到障碍物,摆球继续向右摆动.用频闪照相机拍到如图所示的单摆运动过程的频闪照片,以下说法正确的是( )
 将一单摆向左拉至水平标志线上,从静止释放,当摆球运动到最低点时,摆线碰到障碍物,摆球继续向右摆动.用频闪照相机拍到如图所示的单摆运动过程的频闪照片,以下说法正确的是( )
将一单摆向左拉至水平标志线上,从静止释放,当摆球运动到最低点时,摆线碰到障碍物,摆球继续向右摆动.用频闪照相机拍到如图所示的单摆运动过程的频闪照片,以下说法正确的是( )| A. | 这个实验说明了动能和势能可以相互转化,转化过程中机械能守恒 | |
| B. | 摆线碰到障碍物前后的摆长之比为9:4 | |
| C. | 摆线经过最低点时,线速度不变,半径减小,摆线张力变大 | |
| D. | 摆线经过最低点时,角速度变大,半径减小,摆线张力不变 |
 一束初速度不计的电子在经U的加速电压加速后,在距两极板等距处垂直进入平行板间的匀强电场,如图所示,若板间距离d,板长l,偏转电极边缘到荧光屏的距离为L,偏转电场只存在于两个偏转电极之间.已知电子质量为m,电荷量为e,求:
一束初速度不计的电子在经U的加速电压加速后,在距两极板等距处垂直进入平行板间的匀强电场,如图所示,若板间距离d,板长l,偏转电极边缘到荧光屏的距离为L,偏转电场只存在于两个偏转电极之间.已知电子质量为m,电荷量为e,求: