题目内容
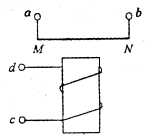
如图所示,金属杆MN放在用相同导体制成的金属框abcd上,bc边与x轴重合,且b为坐标原点,矩形框长为2L,宽为L,单位长度的电阻为R0,磁感应强度为B的匀强磁场与框架平面垂直.现对MN杆施加沿x轴正方向的外力,使之从框架左端开始,以速度v向右匀速运动,不计摩擦.求:
(1)在MN杆运动过程中,通过杆的电流与坐标x的关系;
(2)作用在MN杆上的外力的最大值与最小值之比.
解析:(1)设在MN杆运动的过程中,任一时刻MN的坐标值为x,杆左侧框架的总电阻为R1,右侧框架的总电阻为R2,则
R1=(L+2x)R0;
R2=[L+2(2L-x)]R0=(5L-2x)R0
杆MN相当于电源,所以回路总电阻为
R=![]() +LR0=
+LR0=![]() +LR0=
+LR0=![]() R0
R0
又MN切割磁感线产生的感应电动势为E=BLv,
所以杆中的电流与坐标x的关系为I=![]() =
=![]() .
.
(2)作用在杆上的外力大小应等于杆受的安培力.由数学知识可知,当x=L时,外电路总电阻最大,此时MN中的电流最小,所受的安培力也最小,此时Imin=![]()
安培力的最小值Fmin=ILB=![]()
当x=0或x=2L时,外电路总电阻最小,此时MN中的电流最大,所受的安培力也最大.此时Imax=![]()
安培力的最大值Fmax=ILB=![]()
所以作用在MN杆上的外力的最大值与
最小值之比为Fmax∶Fmin=15∶11.
答案:(1)I=![]()
(2)15∶11

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
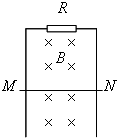 如图所示,金属杆MN,在竖直平面内贴着光滑平行金属导轨下滑,导轨的间距l=10cm,导轨上端接有R=0.5Ω的电阻,导轨与金属杆的电阻不计,整个装置处于B=0.5T的水平匀强磁场中,磁场方向垂直于导轨平面.当金属杆MN下滑时,每秒钟有0.02J的重力势能减少,求MN杆下滑的速度的大小(不计空气阻力).
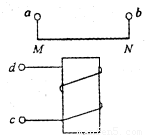
如图所示,金属杆MN,在竖直平面内贴着光滑平行金属导轨下滑,导轨的间距l=10cm,导轨上端接有R=0.5Ω的电阻,导轨与金属杆的电阻不计,整个装置处于B=0.5T的水平匀强磁场中,磁场方向垂直于导轨平面.当金属杆MN下滑时,每秒钟有0.02J的重力势能减少,求MN杆下滑的速度的大小(不计空气阻力).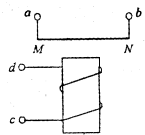 (2009?杨浦区模拟)如图所示,金属杆MN水平固定于线圈上方,杆的两端接有导线.心与线圈轴线处于同一竖直平面内,现将四个接线柱a、b和c、d分别与直流电源的正、负极相接,下列说法中正确的是( )
(2009?杨浦区模拟)如图所示,金属杆MN水平固定于线圈上方,杆的两端接有导线.心与线圈轴线处于同一竖直平面内,现将四个接线柱a、b和c、d分别与直流电源的正、负极相接,下列说法中正确的是( )