题目内容
11.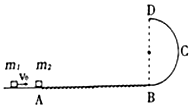 如图所示,水平轨道A点左侧光滑,右侧粗糙,距A点s=1.0m的B端与半径R=0.25m的光滑半圆轨道BCD相切,半圆的直径BD竖直.一小物块m1以v0=3.0m/s的速度,与静置于A点的小物块m2发生弹性碰撞.碰后m2沿水平轨道运动,然后滑上轨道BCD.已知m2=2.0kg,m2与AB轨道间的动摩擦因数μ=0.20,g取10m/s2.
如图所示,水平轨道A点左侧光滑,右侧粗糙,距A点s=1.0m的B端与半径R=0.25m的光滑半圆轨道BCD相切,半圆的直径BD竖直.一小物块m1以v0=3.0m/s的速度,与静置于A点的小物块m2发生弹性碰撞.碰后m2沿水平轨道运动,然后滑上轨道BCD.已知m2=2.0kg,m2与AB轨道间的动摩擦因数μ=0.20,g取10m/s2.(1)若物块m2进入半圆轨道的B点时对轨道的压力大小为68N,求物块m2到达半圆轨道的中点C点时的速度大小VC;
(2)若物块m2能滑上圆轨道,且仍能沿圆轨道滑下,求物块m2碰后的最大速度V1;
(3)若物块m2能滑上圆轨道,且仍能沿圆轨道滑下,求物块m1的质量取值范围.
分析 (1)由牛顿第三定律知,物块刚进入圆轨道时受到的支持力N=68N,由机械能守恒定律结合牛顿第二定律列式求解即可;
(2)要使m2仍能沿圆轨道滑回,m2在圆轨道的上升高度不能超过半圆轨道的中点C,应用动能定理可以求出m2碰后的速度;
(3)碰撞过程动量守恒、机械能守恒,应用动量守恒定律以及机械能守恒定律可以求出m2的质量范围.
解答 解:(1)由牛顿第三定律知,物块刚进入圆轨道时受到的支持力N=68N,
设物块m2经过B点时的速度为vB,
由机械能守恒定律得:$\frac{1}{2}{m}_{2}{{v}_{B}}^{2}=\frac{1}{2}{m}_{2}{{v}_{C}}^{2}+{m}_{2}gR$…①
由牛顿第二定律得:$N-{m}_{2}g={m}_{2}\frac{{{v}_{B}}^{2}}{R}$…②
解得物块m2到达半圆轨道的中点C点时的速度大小为:vC=1.0m/s
(2)要使m2仍能沿圆轨道滑回,m2在圆轨道的上升高度不能超过半圆轨道的中点C,
设碰后m2的速度为v1时恰能滑到C点,由动能定理有:$-μ{m}_{2}gs-{m}_{2}gR=0-\frac{1}{2}{m}_{2}{{v}_{1}}^{2}$…③
解得:v1=3.0m/s(此为m2碰后的最大速度)
(3)设碰后m2的速度为v2时恰能滑到B点,由动能定理有:$-μ{m}_{2}gs=0-\frac{1}{2}{m}_{2}{{v}_{2}}^{2}$
解得:v2=2.0m/s碰后m2的速度满足2.0m/s<v≤3.0m/s时,m2能滑上圆轨道,并仍能沿圆轨道滑下
设 m1、m2发生弹性碰撞后的速度分别为v1′、v2′,以m1的初速度方向为正方向,根据动量守恒定律得:m1v0=m1v1′+m2v2′,
碰撞过程无动能损失,有:$\frac{1}{2}{m}_{1}{{v}_{0}}^{2}=\frac{1}{2}{m}_{1}{v}_{1}{′}^{2}+\frac{1}{2}{m}_{2}{v}_{2}{′}^{2}$
得:${v}_{2}′=\frac{2{m}_{1}}{{m}_{1}+{m}_{2}}{v}_{0}$,
由2.0m/s<$\frac{2{m}_{1}}{{m}_{1}+{m}_{2}}{v}_{0}$≤3.0m/s,
解得:1.0kg<m1≤2.0kg.
答:(1)若物块m2进入半圆轨道的B点时对轨道的压力大小为68N,求物块m2到达半圆轨道的中点C点时的速度大小VC;
(2)若物块m2能滑上圆轨道,且仍能沿圆轨道滑下,求物块m2碰后的最大速度V1;
(3)若物块m2能滑上圆轨道,且仍能沿圆轨道滑下,求物块m1的质量取值范围.
点评 本题考查了求压力、速度与质量范围问题,分析清楚物体运动过程是解题的前提与关键,分析清楚物体运动过程后应用动量守恒定律、动能定理、机械能守恒定律可以解题.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案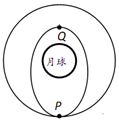 嫦娥三号绕月球做匀速圆周运动,当运动到p点时释放一个探索器(探索器质量为m),探索器绕椭圆轨道运动.(释放时认为嫦娥三号的速度不变能在原轨道运动),月球的质量为M,Q点到月球中心的距离为r,P点到月球中心的距离为R.下列说法正确的是( )
嫦娥三号绕月球做匀速圆周运动,当运动到p点时释放一个探索器(探索器质量为m),探索器绕椭圆轨道运动.(释放时认为嫦娥三号的速度不变能在原轨道运动),月球的质量为M,Q点到月球中心的距离为r,P点到月球中心的距离为R.下列说法正确的是( )| A. | 嫦娥三号运行的周期比探索器运行的周期要大 | |
| B. | 探索器在Q点时的向心力等于G$\frac{Mm}{{r}^{2}}$ | |
| C. | 嫦娥三号做匀速圆周运动的速度大小为$\sqrt{\frac{GM}{R}}$ | |
| D. | 探索器从Q点运动到P点的过程中速率不断变小 |
| A. | 伽利略通过理想斜面实验,提出了力是维持物体运动状态的原因 | |
| B. | 法拉第为了解释磁体产生的磁场提出了分子电流假说 | |
| C. | 楞次在对理论基础和实验资料进行严格分析后,提出了电磁感应定律 | |
| D. | 奥斯特发现了电流周围存在磁场,提出了电流的磁效应 |
| A. | 第二类永动机不能制成是因为自然界中进行的涉及热现象的宏观过程都具有方向性 | |
| B. | 夏天荷叶上小水珠呈球状是由于液体表面张力使其表面积具有收缩到最小趋势的缘故 | |
| C. | 气体的压强是由气体分子的重力产生的,在完全失重的情况下,密闭容器内的气体没有压强 | |
| D. | 对一定量的气体,在压强不断增大的过程,外界对气体一定做功 | |
| E. | 布朗运行是悬浮在液体中的固体微粒的运动,它说明液体分子永不停息地做无规则运动 |
| A. | 1g100℃的水的内能小于1g100℃的水蒸气的内能 | |
| B. | 气体压强的大小跟气体分子的平均动能、分子的密集程度这两个因素有关 | |
| C. | 热力学过程中不可避免地出现能量耗散现象,能量耗散不符合热力学第二定律 | |
| D. | 第二类永动机不可能制成是因为它违反了能量守恒定律 | |
| E. | 某种液体的饱和蒸汽压与温度有关 |
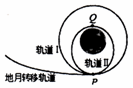 2013年12月,“嫦娥三号”携带月球车“玉兔”从距月面高度为100km的环月圆轨道Ⅰ上的P点变轨,进入近月点为15km的椭圆轨道Ⅱ,经各种控制后于近月点Q成功落月,如图所示.关于“嫦娥三号”,下列说法正确的是( )
2013年12月,“嫦娥三号”携带月球车“玉兔”从距月面高度为100km的环月圆轨道Ⅰ上的P点变轨,进入近月点为15km的椭圆轨道Ⅱ,经各种控制后于近月点Q成功落月,如图所示.关于“嫦娥三号”,下列说法正确的是( )| A. | 沿轨道Ⅱ运行的周期大于沿轨道Ⅰ运行的周期 | |
| B. | 在轨道Ⅰ上经P点的速度大于在轨道Ⅱ上经P点的速度 | |
| C. | 在轨道Ⅱ上由P点到Q点的过程中机械能增加 | |
| D. | 沿轨道Ⅱ运行时,在P点的加速度大于在Q点的加速度 |
 利用如图所示的电路研究光电效应现象,其中电极K由金属钾制成,其逸出功为2.25eV.用某一频率的光照射时,逸出光电子的最大初动能为1.50eV,电流表的示数为I.已知普朗克常数约为6.6×10-34Js,下列说法正确的是( )
利用如图所示的电路研究光电效应现象,其中电极K由金属钾制成,其逸出功为2.25eV.用某一频率的光照射时,逸出光电子的最大初动能为1.50eV,电流表的示数为I.已知普朗克常数约为6.6×10-34Js,下列说法正确的是( )| A. | 金属钾发生光电效应的极限频率约为5.5×1014Hz | |
| B. | 若入射光频率加倍,光电子的最大初动能变为3.00eV | |
| C. | 若入射光频率加倍,电流表的示数变为2I | |
| D. | 若入射光频率加倍,遏止电压的大小将变为5.25V |
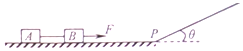 如图所示,足够长的倾角θ=37°的斜面与水平地面在P点平滑连接,通过轻绳连接的A、B两物体静置于水平地面上,质量分别为m1=2kg,m2=4kg,此时轻绳处于水平且无拉力,物体A与接触面之间的动摩擦因数均为μ1=0.5,物体B与接触面之间的动摩擦因数均为μ2=0.75,对物体B施加水平恒力F=76N,使两物体一起向右加速运动,经过时间t=2s物体B到达斜面底端P点,此时撤去恒力F,若两物体均可视为质点,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.
如图所示,足够长的倾角θ=37°的斜面与水平地面在P点平滑连接,通过轻绳连接的A、B两物体静置于水平地面上,质量分别为m1=2kg,m2=4kg,此时轻绳处于水平且无拉力,物体A与接触面之间的动摩擦因数均为μ1=0.5,物体B与接触面之间的动摩擦因数均为μ2=0.75,对物体B施加水平恒力F=76N,使两物体一起向右加速运动,经过时间t=2s物体B到达斜面底端P点,此时撤去恒力F,若两物体均可视为质点,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8. 如图所示.小木箱ABCD的质量M=2.2kg,高L=1.0m,其顶部离挡板E的距离h=2.0m,木箱底部有一质量m=0.8kg的小物体P.在竖直向上的恒力T作用下,木箱向上运动,为了防止木箱与挡板碰撞后停止运动时小物体与木箱顶部相撞.求拉力T的最大值.
如图所示.小木箱ABCD的质量M=2.2kg,高L=1.0m,其顶部离挡板E的距离h=2.0m,木箱底部有一质量m=0.8kg的小物体P.在竖直向上的恒力T作用下,木箱向上运动,为了防止木箱与挡板碰撞后停止运动时小物体与木箱顶部相撞.求拉力T的最大值.